Consignes
Le TP est à rendre (par email) pour le 15 décembre à 23h59.
D'autre part, chaque groupe devra, en fin de séance, faire une démonstration de ses fonctions sur des exemples biens choisis. Tous les membres du groupes devront y prendre part.
La pièce la plus importante sera un fichier tp3-nom-prenom.c contenant votre programme. Le seul fait que votre programme fonctionne ne suffit pas pour avoir une bonne note. Les points suivants seront également pris en compte :
- la lisibilité de votre programme (choix pertinent pour les noms de variables, indentation etc.),
- la présence de commentaires aux endroits appropriés,
- ...
Les réponses aux questions posées dans le TP (complexité de vos fonctions par exemple) seront insérées comme commentaires dans votre fichier principal.
Si vous le souhaitez, vous pouvez aussi envoyer un rapport de TP. Le format de ce rapport sera au choix, mais par ordre de préférence :
- dans le corps de votre programme en commentaire,
- au format texte (mais avec un minimum de mise en page),
- au format pdf,
- au format OpenOffice (
.odt), - au format Word (beurk).
Attention : les points suivants ne rapportent rien, mais ne pas les respecter pourra retrancher jusqu'à 10 points sur la note finale :
- chaque fichier devra comporter un commentaire au début avec vos nom, prénom, filière, intitulé du cours et numéro du TP,
- votre code final devra compiler avec les options de compilation
-Wall -Werror -Wextra -pedantic -std=c99 - une exécution du programme de test fourni ne devra pas provoquer d'erreur.
Estimation du temps
- algorithme de Prim (question 1) : 1h,
- génération de labyrinthes (questions 2, 3 et 4) : 1h,
- algorithme de Dijkstra : 1h30,
- tests et conclusions : 30min.
Liens utiles
- l'archive contenant les fichiers nécessaires pour le TP
- le TP1, avec quelques explications sur la bibliothèque fournie
- le TP2
- emails des encadrants de TP : Pierre.Hyvernat@univ-savoie.fr et Xavier.Provencal@univ-savoie.fr.
Préliminaires
- Téléchargez l'archive du TP.
- La compilation se fait avec le fichier
Makefilefourni comme pour le TP1. Il suffit de modifier la variableNOMpour prendre en compte votre propre fichier. - Aucune fonction de test n'est fournie pour ce TP. Vous devrez donc vous débrouiller pour tester vos fonctions au fur et à mesure. (Par contre, ce n'est pas la peine de m'envoyer votre fonction principale.)
La structure de "grapheListe" de la librairie fournie permet de gérer facilement les graphes pondérés (avec des poids entiers sur les arcs). En effet, si "L" est la liste d'adjacence du sommet "u", on accède :
- au premier voisin avec "
L->but", - au poids de l'arc correspondant avec "
L->poids", - à la liste des autres voisins avec "
L->suivant".
1. Algorithme de Prim
L'algorithme de Prim, vu en cours et en TD permet de calculer un arbre couvrant de poids minimal dans un graphe non-orienté pondéré. En langage algorithmique, l'algorithme est :
/* initialisation
* - poids_A[] est un tableau de taille n
* - pere[] est un tableau de taille n
* - etat[] est un tableau de taille n
*/
pour chaque sommet s :
poids_A[s] := +∞
pere[s] := -1
etat[s] := non_vu
fin pour
a_traiter := 0 /* choix arbitraire de sommet initial */
etat[a_traiter] := vu
i := 1 /* nombre de sommets dans l'arbre courant */
pour chaque voisin v de a_traiter :
poids_A[v] := poids(a_traiter,v)
pere[v] := a_traiter
fin pour
/* boucle principale */
tant que i<n :
/* recherche du minimum */
min := +∞
pour chaque sommet s :
si etat[s] == non_vu
alors
si poids_A[s] < min
alors
min := poids_A[s]
a_traiter := s
fin si
fin si
fin pour
etat[a_traiter] := vu
i := i+1
/* mise à jours des voisins de a_traiter */
pour chaque voisin v de a_traiter :
si etat[v] == non_vu
alors
si poids(a_traiter,v) < poids_A[v]
alors
poids_A[v] := poids(a_traiter,v)
pere[v] := a_traiter
fin si
fin si
fin pour
fin tant que
Programmez la fonction suivante :
GrapheListe prim (GrapheListe G) ;
Attention : vous devez générer un "GrapheListe" et non pas un tableau comme dans l'algorithme vu en cours. Le plus simple reste pourtant de créer le tableau "pere", et seulement à la fin, de le convertir en "GrapheListe". (Sinon, il ne faut pas oublier de supprimer les arcs qui ne servent plus lorqu'on change le prédécesseur d'un sommets.)
2. Génération de labyrinthes
Comme vu dans le TP1, un labyrinthe est généralement un arbre car :
- il est connexe,
- il n'y a qu'un seul chemin pour aller d'un endroit à un autre.
2.1. Arbre couvrant minimal
Si on part d'un graphe connexe, on peut donc générer un labyrinthe en calculant un arbre couvrant. En particulier, si chaque sommet représente une pièce et chaque arête représente une porte, les deux exemples de graphes suivants peuvent générer les deux labyrinthes suivants :
__ __ __ __ __ __ __ __ __ __
+--+--+--+--+--+--+--+--+--+--+ / \__/ \__/ \__/ \__/ \__/ \__/ \__/ \__/ \__/ \__
| | \ \
+ + + + + + + + + + + / /
| | \ \
+ + + + + + + + + + + / /
| | \ \
+ + + + + + + + + + + / /
| | \ \
+ + + + + + + + + + + / /
| | \ \
+ + + + + + + + + + + / /
| | \ \
+ + + + + + + + + + + / /
| | \ \
+ + + + + + + + + + + / /
| | \ \
+ + + + + + + + + + + / /
| | \ \
+ + + + + + + + + + + / /
| | \__ __ __ __ __ __ __ __ __ __ \
+--+--+--+--+--+--+--+--+--+--+ \__/ \__/ \__/ \__/ \__/ \__/ \__/ \__/ \__/ \__/
__ __ __ __ __ __ __ __ __ __
+--+--+--+--+--+--+--+--+--+--+ / \__/ \__/ \__/ \__/ \__/ \__/ \__/ \__/ \__/ \__
| | | \ __/ __/ __/ __/ __/ __/ __/ \__ __ \
+ +--+ + +--+ + +--+--+ + / \__ \ / \__ __ __/ \ __ \__ __/ \ /
| | | | | | | | \__/ / \__ __/ __ __ \ / \__/ \ \ / \
+ +--+ + + +--+--+ +--+ + / \__/ __/ __/ \__/ \__/ __/ __ \ / \ / \__/
| | | | | | | \ \ / \ / __ \__/ \__/ \__ \__/ \
+ + +--+ + + + +--+ +--+ / \__/ __/ \ / / \__ \ / \ / \__/ \__/ \ /
| | | | | | | | \__ \ / \__/ \__/ \__ \ \__ \ / \__ __/ \
+ +--+ + +--+--+ +--+--+ + / \ / \ / \__ \ / \ \__/ __ \__ \ / __/
| | | | | | \__ \ / / \ / \ / \__ \__/ / \ / \__/ \
+ +--+--+--+ + +--+ +--+ + / \ __/ \__ \__ \ / \__ \__/ \ / \ / __/
| | | | | | | \__ \__/ __/ __/ \ / \ / \__/ \ \__ __/ \
+ + +--+ +--+ + +--+ + + / \ / \__ __ \ \__ \__ \__/ __/ \ /
| | | | | | | \__ __/ \__/ __/ \__/ \__/ \ / \ / __/ / \
+ + +--+ +--+ +--+--+--+ + / __/ \__ \ \__ __ __ \__/ \ / \ / \ /
| | | | | | | \__ __/ \__ \__/ \__/ \__ \__/ \__/ __/ \__ \
+--+ +--+--+ + + +--+ + + / \__ __ \__/ / \__ __/ \__ __ __ \ /
| | | | \ \ / / \__/ \__ / __ \ / \__/ \
+--+--+ + +--+--+ +--+ + + / \__ \__/ \ \ / \__/ \__/ \ \ / / \ /
| | | | | | \__ \__ \__ \__ __/ __ \__ \__/ \__/ __/ \
+--+--+--+--+--+--+--+--+--+--+ \__/ \__/ \__/ \__/ \__/ \__/ \__/ \__/ \__/ \__/
Pour que les labyrinthes générés ne soient pas tous identiques, une possibilité est d'allouer des poids aléatoires aux arêtes et de calculer un arbre couvrant minimal.
Générez des labyrinthes aléatoires en utilisant des graphes aléatoires (fonctions grilleRectPleine et grilleHexPleine).
Comparez vos labyrinthes avec ceux générés par les fonctions labyrintheRect et labyrintheHex qui utilisent l'algorithme de Kruskal. Qu'en pensez-vous ?
2.2. Arbre couvrant aléatoire
Une autre manière de calculer un arbre couvrant est simplement d'utiliser un parcours, en largeur ou profondeur. Pour introduire de l'aléatoire, il suffit que les listes d'adjacences ne soient pas triées par numéro de sommet. Les graphes produits par "grilleRectPleine" ou "grilleHexPleine" ont justement leurs listes d'adjacences triées par poids croissant. Comme le poids est aléatoire, cela provoque des parcours en profondeur / largeur imprévisibles.
Écrivez une fonction
GrapheListe profondeur (GrapheListe G) ;
Utilisez cette fonction pour générer des labyrinthes, et comparez les avec ceux obtenus auparavant.
Même question avec un parcours en largeur : écrivez une fonction
GrapheListe largeur (GrapheListe G) ;
Utilisez cette fonction pour générer des labyrinthes, et comparez les avec ceux obtenus auparavant.
Qu'en pensez-vous ?
2.3. Complexité
Comparez les temps d'exécution de votre fonction "prim" et de la fonction "kruskal" sur des gros graphes (fonction "grapheListeAleatoire").
Qu'en pensez-vous ?
(bonus)
- La recherche du minimum se fait en parcourant tous les sommets. On pourrait conserver une liste des sommets voisins de l'arbre en construction (ceux qui ont un "
pere[]" définie) pour améliorer la complexité en pratique. Faites le... - Mieux : implantez une structure de tas pour optimiser la partie
/* recherche du minimum */dans l'algorithme de Prim.
3. Chemin couvrant minimal, algorithme de Dijkstra
Lorsqu'un graphe est pondéré, la distance naturelle entre deux sommets est naturellement le minimum des sommes des poids des arêtes pour les chemins entre les deux sommets. Sur le dessin suivant :
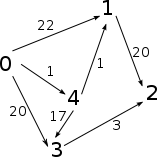 |
on a les distances suivantes :
- distance de "
0" à "1" : 2, - distance de "
3" à "2" : 3, - distance de "
0" à "2" : 21, - ...
Lorsque le graphe a des poids négatifs, ce minimum n'existe pas forcément :
 |
L'algorithme de Disjkstra ressemble à l'algorithme de Prim mais permet de calculer les distances d'un sommet vers tous les autres. Il fonctionne de la manière suivante : pour calculer les distances à partir du sommet "s", on parcourt le graphe en partant de "s". Comme pour l'algorithme de Prim, on construit un arbre en gardant en mémoire comment les voisins de l'arbre sont reliés à l'arbre ; mais au lieu de garder seulement le poids de l'arc entre "v" et "pere[v]", on conserve « la distance minimale courante pour aller de "s" à "v".
Si on garde la même structure que pour l'algorithme de Prim donné plus haut, on utilisera donc :
- un tableau "
etat[]" pour conserver l'état des sommets :- "
VU" pour ceux dont on connaît la distance à partir de "s", - "
NON_VU" pour ceux dont on n'est pas encore sûr de la distance à partir de "s".
- "
- un tableau "
distances[]" contenant- la distances minimale depuis "
s" pour les sommets dont l'état est "VU", - la distance minimale courante depuis "
s" pour les sommets dont l'état est "NON_VU".
- la distances minimale depuis "
- un tableau "
pere[]" pour conserver- l'arbre que l'on construit (pour les sommets dont l'état est "
VU") - le plus court chemin courant pour accéder jusqu'au sommet (pour les sommets dont l'état est "
NON_VU".) Dans ce cas, le plus court chemin temporaire est simplement de suivre le tableau "pere[]".
- l'arbre que l'on construit (pour les sommets dont l'état est "
Faites tourner l'algorithme de Dijkstra à la main sur le premier graphe, puis sur d'autres exemples de votre choix.
Écrivez la fonction correspondante :
int * dijkstra (GrapheListe G, int depart) ;
Consignes :
- votre fonction devra renvoyer un tableau contenant les distances à partir du sommet "
depart" (ou-1si le sommet n'est pas accessible), - inspirez-vous de l'algorithme de Prim donné au début du TP,
- n'essayez pas d'optimiser votre code avant d'être sûr d'avoir une version qui fonctionne,
- proposez des optimisations possibles pour votre algorithme.


