Consignes
La partie obligatoire de ce TP sera notée par votre intervenant pendant la séance de TP. Vous devrez donc appeler votre intervenant à chaque fois que vous avez terminé une question.
Les questions « bonus » peuvent être envoyée par email à votre intervenant pendant la semaine (7 jours) qui suivent votre séance de TP. N'oubliez pas de mettre votre nom ainsi que votre filière en commentaire dans les fichiers que vous nous envoyez...
Attention : pour que les questions bonus soient prises en compte, il faut que les questions obligatoires aient été traitées. Si vous n'avez pas fini les questions obligatoires en TP, il faut donc les finir chez vous avant de traiter les questions bonus...
La note ne valide pas seulement le résultat de votre programme, mais également son style :
- choix approprié des noms de variables,
- présence de documentation pour les fonctions importantes,
- commentaires pertinents (la paraphrase de code, par exemple:
y = x * 2 # y est le double de xn'apporte rien), - découpage des fonctions / procédures complexes en sous-fonctions / sous-procédures lorsque nécessaire...
Vérifiez ces points avant de demander à votre intervenant de valider votre code.
Liens utiles
- la page du langage Python
- la page de la documentation de la librairie standard de Python
- un livre d'apprentissage de la programmation en Python (en français) (lien direct (pdf))
- email des enseignants
- Chambéry : Pierre.Hyvernat@univ-savoie.fr (cours, TD et TP), Thomas.Seiller@univ-savoie.fr (TD et TP) et tom.hirschowitz@univ-savoie.fr (TP),
- Annecy : Christophe.Raffalli@univ-savoie.fr (cours, TD et TP), lionel.valet@univ-savoie.fr (TD et TP) et Ilham.Alloui@univ-savoie.fr (TP).
D'autre part, vous aurez besoins des fichiers suivant pour ce TP :
- le fichier à trous pour la partie 1 : boulet.py
- le fichier à trous pour la partie 2 : frac-poly.py
Préliminaires
Le but de ce TP est de revoir certains concepts vu au premier semestre (boucles, conditionnelles, fonctions) en insistant sur la qualité du code écrit. Pour ceci, il faudra suivre les règles vues en cours concernant :
- la documentation des fonctions importantes (docstrings de Python),
- des choix appropriés pour les noms de vos variables et arguments de vos fonctions,
- utilisation de valeurs par défaut pour certains arguments de vos fonctions,
- présence de commentaires pertinents (caractère
#de Python),
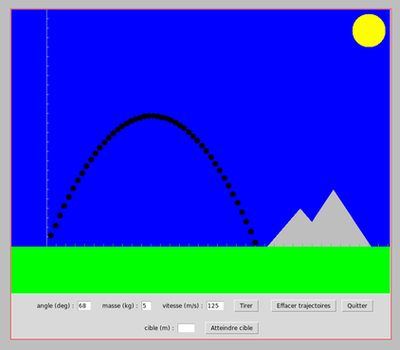
Dans la première partie, nous allons modéliser (et dessiner) la trajectoire d'un boulet de canon en fonction de l'angle de tir, de la vitesse initiale du boulet et de sa masse. Nous chercherons ensuite à ajuster automatiquement l'angle de tir pour essayer d'atteindre une cible précise.
Dans la seconde partie, nous utiliserons une méthode itérative pour calculer les zéros d'un polynôme dans les nombres complexes. Le comportement de cette méthode sur les points du plan permettra de dessiner des fractales bien connues des mathématiciens.
 |
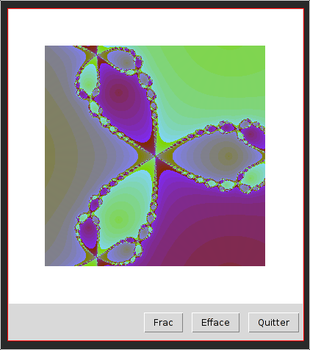 |
| partie 1 | partie 2 |
1. Un boulet de canon...
1.1. Modélisation de la trajectoire
La trajectoire d'un objet inerte est régie par les lois de la mécanique. Nous allons utiliser une approximation de ces lois pour modéliser de manière discrète la trajectoire d'un boulet de canon.
À un instant t donné, le boulet a
- une position (x(t),y(t)),
- une vitesse (vecteur) (vx(t),vy(t))
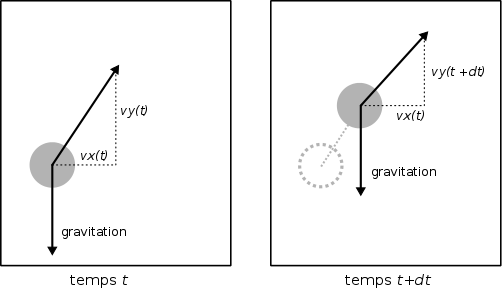
et il est soumis à la force d'attraction terrestre. Au temps t + ε, la position du boulet ainsi que sa vitesse seront modifiées en utilisant les formules
- x(t+ε) = x + vx(t) * ε,
- y(t+ε) = y + vy(t) * ε,
- vx(t+ε) = vx(t), car on néglige les frottements,
- vy(t+ε) = vy(t) - m * G * ε, où m est la masse du boulet et G est la constante gravitationnelle de la terre (9.81).
 |
Pour que la modélisation ressemble à la réalité physique, il faut que ε soit assez petit.
Écrivez une fonction "trajectoire_boulet" qui prend en argument les valeurs suivantes :
angle: l'angle du canon, en degrés, par rapport à l'horizontalmasse: la masse, en kilogramme, du boulet de canon (5kg est une valeur pertinente)vitesse: la vitesse, en mètre/s, du boulet à la sortie du canon (125 m/s est une valeur pertinente).dt: la valeur ε, en centièmes de secondes. Si cette valeur n'est pas fournie, votre fonction utilisera la valeur1par défaut.freq: la fréquence des affichages. En effet, si l'on dessine le boulet trop souvent, on ne pourra pas voir les positions successive du boulet. Une valeur de se paramètre de 50 n'affichera donc qu'une position sur 50. Si cette valeur n'est pas donnée, votre fonction utilisera la valeur10par défaut.
Votre fonction devra calculer toutes les valeurs successive du boulet jusqu'à ce qu'il atteigne le sol. Elle affichera (en utilisant la fonction dessine_boulet(x,y)) le boulet à la fréquence demandée.
- Vous devez écrire votre fonction dans le fichier à trous boulet.py.
- Le fichier fourni comporte une ligne
Vous pouvez donc utiliser les fonctions sinus et cosinus, ainsi que la constante π. Attention, les fonction trigonométrique de Python utilisent des angles en radians, alors que votre fonction utilise un angle en degrés...
from math import sin,cos,pi
- Pour tester votre fonction, il suffit de lancer Python sur le fichier (menu
"Run" -> "Run Module F5") et d'utiliser la petite interface.
1.2. Recherche dichotomique de l'angle pour atteindre une cible
Nous cherchons maintenant à atteindre une cible, avec une précision de 1 mètre. Pour ceci, il faudra tirer des boulets (avec la fonction trajectoire_boulet) et modifier l'angle en fonction de la distance parcourue par le boulet :
- on commence par tirer un boulet à 45° ; et si la distance est trop courte, c'est qu'on ne pourra pas l'atteindre. On s'arrête...
- Sinon, et si on n'a pas atteint la cible, on diminue l'angle de moitié et on essaie de tirer à 22.5°. Suivant que le boulet tombe trop prêt ou trop loin, on choisira ensuite de tirer à 33.75° ou 11.25°. On continue jusqu'à atteindre la cible...
Le principe général d'une recherche dichotomique est de diviser son espace de recherche par deux à chaque étape. Au début, on sait simplement que l'angle cherché est entre 45° et 0° ; ensuite, qu'il est entre (par exemple) 45° et 22.5° ; ensuite, qu'il est entre (par exemple) 33.75° et 22.5°, etc.
Écrivez la fonction dichotomie, qui prend en argument :
cible: la distance entre le canon et la cible, en mètres,masse,vitesse,dtetfreqavec la même interprétation que dans la question précédente.
Votre fonction appellera la fonction précédente trajectoire pour calculer et afficher les trajectoires du boulet.
Vous pouvez essayer de tirer « en cloche » en choisissant des angles entre 45° et 90°, ou « ras le sol » en choisissant des angles entre 0° et 45°.
2. Des fractales avec des polynômes...
La méthode de Newton est une méthode pour calculer des approximations de plus en plus précises de solutions d'équations de la forme f(z) = 0, où f est une « bonne fonction ». Nous allons nous intéresser au cas où f est un polynôme, et dans un premier temps, au cas où f(z) = z3 + 1.
La méthode de Newton fonctionne de la manière suivante : sous les bonnes hypothèses,
- si z0 est une approximation d'une solution de f(z)=0,
- alors z1 = z0 - f(z0) / f'(z0), où f' est la dérivée de f, est une meilleure approximation de la solution.
On peut ainsi calculer des approximations x2, ..., xn de plus en plus précises. Vous pouvez consulter la page Wikipedia sur la méthode de Newton pour plus de détails.
Pour cette partie, vous aurez besoin du fichier à trous suivant : frac-poly.py.
2.1. polynômes et nombres complexes
Python possède un type spécial pour les nombres complexes :
Python 3.1.3 (r313:86834, Nov 28 2010, 10:01:07)
[GCC 4.4.5] on linux2
Type "help", "copyright", "credits" or "license" for more information.
>>> z = complex(1,2)
(1+2j)
>>> type(z)
<class 'complex'>
>>> z*z
(-3+4j)
>>> print("La partie réelle de z est", z.real, "et sa partie imaginaire est", z.imag)
La partie réelle de z est 1.0 et sa partie imaginaire est 2.0
Les points importants sont :
- pour déclarer un nombre complexe, on utilise
z = complex(partie_réelle, partie_imaginaire) - on peut utiliser les opérations habituelles sur les nombres flottants :
+,*,/, ... - on peut accéder à la partie réelle d'un nombre complexe
zavecz.real, et à sa partie imaginaire avecz.imag. - Python utilise la lettre
jau lieu de la lettre i habituellement utilisée par les mathématiciens.
Écrivez une (mini) fonction module qui calcule le module d'un nombre complexe.
Un polynôme est donné par le tableau de ses coefficients. Un polynôme est donc simplement un tableau de nombres complexes, où la case d'indice 0 est le terme constant, et la dernière case est le coefficient du monôme de plus haut degré...
Par exemple, le polynôme z3 + i = i + 0 z + 0 z2 + 1 z3 est représenté par [complex(0,1) , complex(0,0) , complex(0,0) , complex(1,0) ].
Écrivez une fonction degre qui renvoie le degré d'un polynôme. La fonction prend un seul argument : P, un polynôme complexe.
Écrivez une fonction evaluePolynome qui calcule la valeur d'un polynôme en un point complexe. Elle prend deux arguments :
P, un polynôme complexe,z, un nombre complexe.
Écrivez une fonction derivePolynome qui calcule le polynôme dérivé d'un autre polynôme. Cette fonction a un unique argument, un polynôme P à dériver...
2.2. La méthode de Newton
Nous avons maintenant tous les ingrédients pour pouvoir programmer la méthode de Newton. Vous devrez calculer des approximations de plus en plus précises, et vous arrêter quand l'une des deux conditions suivantes est satisfaite :
- l'approximation est, à
epsilonprêt, une solution de l'équation f(zi) = 0 - on a déjà calculé au
max_iterationsapproximations.
Écrivez la fonction newton qui prend 5 arguments :
Pun polynôme complexe,dP, le polynôme dérivé du précèdent,z, un nombre complexe représentant l'approximation initiale de la solution,epsilon, un nombre réel, petit, spécifiant la précision que l'on souhaite obtenir (1e-10est une bonne valeur par défaut),max_iterations, le nombre maximal d'approximations que l'on calcule.
La fonction doit renvoyer une paire (i,z), où
iest le nombre d'itérations faites, ou-1si l'on a dépassémax_iterationsitérations,zest la dernière approximation calculée.


