Consignes
Si certains exercices n'ont pas pu être terminés dans le cadre de cette séance, il est fortement conseillé de les terminer par vous-même chez vous ou en salle libre service.
Liens utiles
- la page du langage Python
- un livre d'apprentissage de la programmation en Python (en français) (lien direct (pdf))
- email des encadrants de TP :
Objectifs du TP
Le but de ce TP est de se familiariser avec les tableaux.
Rappels : les tableaux
Testez les lignes suivantes directement dans l'interpréteur Python, et vérifiez que vous comprenez bien chacune des lignes.
>>> t1 = [2, 4, 6, 8] # on déclare un tableau à 4 cases >>> len(t1) # sa taille ??? >>> t2 = t1 + [8, 10] # on concatène le tableau avec un nouveau tableau >>> len(t2) # taille du nouveau tableau ??? >>> t2[0] # la première case ??? >>> t2 # le tableau t2 ??? >>> t2[4] = 12 # on modifie une case par une affectation >>> t2 # le tableau t2 ??? >>> t2 * 2 ???
Les polynômes
On représentera un polynôme avec un tableau de flottants contenant ses coefficients. Le coefficient de degré i se trouvera dans la case d'indice i.
Par exemple, le polynôme 2.3 + 4.9 X + 8.6 X3 sera représenté par le tableau [2.3, 4.9, 0, 8.6]. Notez bien que la case d'indice 0 correspond au terme constant. Un polynôme de degré d aura donc une taille de d+1.
Évaluation d'un polynôme
Écrivez une fonction calcule_polynome qui prend deux arguments :
- un polynôme
P(c'est à dire un tableau), - un nombre
x.
Votre fonction doit renvoyer la valeur du polynôme P sur la valeur x.
Par exemple, le polynôme 1 + 3X + X2 (donné par le tableau [1,3,1] prend
- la valeur 1 sur le nombre 0,
- la valeur 5 sur le nombre 1,
- la valeur -1 sur le nombre -1,
- la valeur 11 sur le nombre 2.
Attention, il faut que votre fonction s'appelle exactement calcule_polynome et qu'elle prenne les deux argument P et x dans cet ordre. Votre fonction sera utilisé par la procédure d'affichage graphique.
Affichage d'un polynôme
Téléchargez le fichier tp4-polynomes.py et recopiez la définitions de calcule_polynome au début du fichier.
Ce fichier contient une procédure d'affichage graphique des polynôme. Cette procédure prend au moins 3 arguments :
- la valeur de
xminimale, - la valeur de
xmaximale, - les polynômes à afficher (au moins 1), sous forme de tableaux.
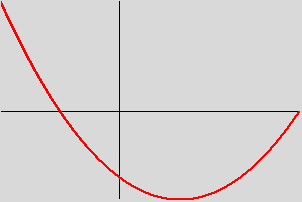
>>> graphe_polynome(-2, 3, [-3,-2,1])
ouvrira une fenêtre avec le graphe du polynôme -3 - 2X + X2 entre -2 et 3 :
 |
Multiplication par un nombre
Écrivez une fonction multiplication_scalaire(P, a) qui multiplie un polynôme par un nombre. Autrement dit, chaque coefficient est multiplié par ce même nombre :
Rappel : le plus simple pour initialisez un tableau de n nombre est d'utiliser :
Q = [0] * n
qui créé un tableau de taille n ne contenant que des 0. Il ne reste plus qu'a modifier les cases du tableau avec une boucle...
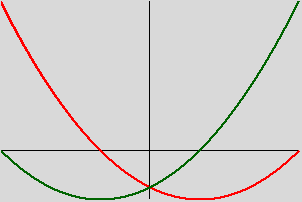
>>> P = [-3,-2,1] >>> graphe_polynome(-2, 3, P, multiplication_scalaire(P, 2))
 |
Opposé d'un polynôme
Écrivez une fonction pour calculer l'opposé d'un polynôme, obtenu en prenant l'opposé de tous les coefficients.
Combien de paramètres cette fonction doit elle avoir ? Quels sont leurs types ? Quel est le type du résultat de cette fonction ?
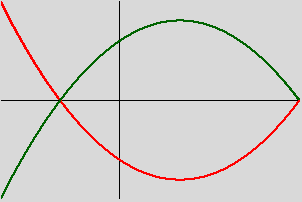
Vérifiez que l'opposé d'un polynôme est bien symétrique par rapport à l'axe des x :
>>> P = [-3,-2,1] >>> graphe_polynome(-2, 3, P, oppose(P))
 |
Écrivez maintenant une fonction qui calcule le symétrique d'un polynôme. Le symétrique ressemble à l'opposé, mais on change seulement les signes des coefficient de degré impair.
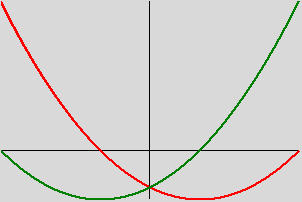
Vérifiez que l'opposé d'un polynôme est bien symétrique par rapport à l'axe des y :
>>> P = [-3,-2,1] >>> graphe_polynome(-3, 3, P, symetrique(P))
 |
Addition de deux polynômes
Écrivez une fonction pour calculer la somme de deux polynômes.
Combien de paramètres cette fonction doit elle avoir ? Quels sont leurs types ? Quel est le type du résultat de cette fonction ?
Attention,
- vous devez pouvoir additionner des polynômes de degré différents,
- n'oubliez pas de tester votre fonction.
Dérivée d'un polynôme
Écrivez une fonction pour calculer la dérivée d'un polynôme.
Testez en dessinant les graphes de polynômes avec leurs dérivées et vérifiez que les maximums et minimums ont bien lieu là où la dérivée s'annule, par exemple avec le polynôme 18 + 3X - 25X2 - 5X3 + 7X4 + 2X5 entre -2.8 et 1.5.
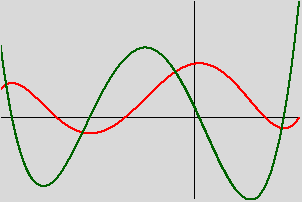 |
Affichage textuel d'un polynôme
Écrivez une qui créé une chaîne de caractère qui représente le polynôme en notation standard :
def chaine_polynome(P):
...
...
Par exemple
>>> chaine_polynome([1,1,2,-3,4,5])
'1*X^0 + 1*X^1 + 2*X^2 + -3*X^3 + 4*X^4 + 5*X^5'
Pour pouvoir ajouter un entier dans une chaîne de caractères, il faut commencer par transformer l'entier en chaîne de caractères. Pour ceci, il faut utiliser la fonction str de python :
>>> 12 12 >>> str(12) '12' >>> "Il y a " + str(12) + " mois dans l'année." "Il y a 12 mois dans l'année."
Facultatif : améliorez votre fonction pour :
- ne pas mettre le "
*X^0" correspondant au coefficient constant, - ne mettre que "
X" au lieu de "X^1" - ne pas mettre les monômes dont le coefficient est
0, - mettre les coefficients négatifs directement avec "
- 2.3 * X^7" au lieu de "+ -2.3 * X^7" - ...
Ainsi, vous aurez :
>>> chaine_polynome([3,6,0,-3,-4,0])
'3 + 6*X - 3*X^3 - 4*X^4'
Si votre fonction porte bien le nom chaine_polynome elle sera utilisée par la procédure d'affichage graphique :
>>> P = [-3,-2,1] >>> graphe_polynome(-2, 3, P, oppose(P)) affichage des polynomes entre x=-2 et x=3 les valeurs varient entre y=-5.0 et y=5.0 rouge : -3 - 2X + X^2 vert : 3 + 2X - X^2 Appuyez sur la touche 'q' pour quitter la fenêtre graphique.
Plus dur
Multiplication
Écrivez (et testez) une fonction qui calcule la multiplication de deux polynômes.
Attention, c'est plus complexe pour l'addition, car le degré du résultat augmente. Par exemple, on a (- 2 + 4X -3X2) (1 - X + X3) = -2 + 6X - 7X2 + X3 + 4X4 - 3X5
Conseils : n'hésitez pas à décomposer le problème en écrivant des fonctions supplémentaires comme mult_poly_monome qui multiplie un polynôme par un monôme...
Composition
Écrivez et testez une fonction qui calcule la composition de deux polynômes.
Exemple de composition :
- P(x) = - 2 + 4x -3x2
- Q(x) = - 1 + 4x
| (P . Q)(x) | = P( Q(x) ) |
| = - 2 + 4(Q(x)) - 3(Q(x))2 | |
| = - 2 + 4(- 1 + 4x) -3(- 1 + 4x)2 | |
| = - 2+ 4(- 1 + 4x)- 3(1- 8x +48x2) | |
| = - 2 - 4+ 16x - 3+ 24x -48x2 | |
| = - 9 + 40x -48x2 |
Conseils : n'hésitez pas à décomposer le problème en écrivant des fonctions supplémentaires comme puissance_polynome qui permet de calculer une puissance d'un polynôme...


