Consignes
Si certains exercices n'ont pas pu être terminés dans le cadre de cette séance, il est fortement conseillé de les terminer par vous-même chez vous ou en salle libre service.
Liens utiles
- la page du langage Python
- un livre d'apprentissage de la programmation en Python (en français) (lien direct (pdf))
- email des encadrants de TP :
Objectifs du TP
Le but de ce TP est d'approfondir votre maîtrise des :
- conditionnelles
- variables et affectations,
- fonctions,
et de commencer à pratiquer les boucles « for ».
Pour ceci, nous utiliserons le débogueur intégré à Idle.
Le débogueur
Un « débogueur » est un outil permettant de ... chercher des bogues dans un programme. Une fonctionnalité intéressante est la possibilité d'exécuter le programme pas à pas en regardant les valeurs des variables à chaque étape.
Pour activer le débogueur de Idle, il suffit de cocher Debugger dans le menu Debug de l'interpréteur. (Pour le désactiver, il faut décocher Debugger...)
Une fois activé, le débogueur ouvrira une fenêtre supplémentaire ressemblant à celle ci :
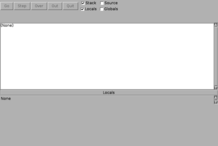 |
Pour notre utilisation, il est préférable de décocher la case "Stack" et de cocher la case "Source".
Positionnez ensuite les trois fenêtre (fichier, interpréteur et débogueur) cote à cote, comme par exemple :
 |
Débogueur en mode « pas à pas »
Lorsque que l'interpréteur évalue une expression, il procède pas à pas : il faut cliquer sur le bouton "Over" (ou "Step") du débogueur pour passer à la ligne suivante. D'autre part, la ligne que l'interpréteur s'apprête à exécuter est surlignée dans le fichier et la valeur des variables locales est affichée dans le débogueur. Par exemple, après quelques pas, on peut obtenir
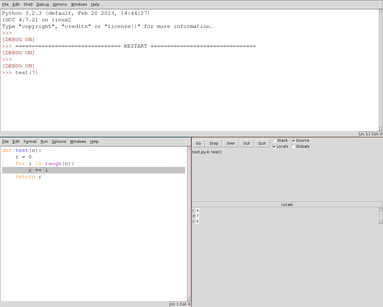 |
Les boutons ont les significations suivantes :
- "Over" : pour exécuter les instructions de la ligne surlignée et passer à la ligne suivante, sans détailler les appels de fonctions. C'est ce bouton que vous utiliserez le plus.
- "Step" : pour exécuter les instructions de la ligne surlignée et passer à la ligne suivante, en détaillant les appels de fonctions.
- "Go" : pour exécuter le programme normalement, jusqu'à un point d'arrêt (voir plus bas).
- "Out" : pour exécuter le programme normalement, jusqu'à ce que la fonction actuelle soit terminée.
- "Quit" : pour arrêter complètement l'exécution.
- Lorsque le débogueur est activé et que vous évaluez votre fichier (touche F5 ou commande
Run Moduledu menuRun), les définitions passent elles-même dans le débogueur. Il convient donc de cliquer sur le bouton "Go" pour évaluer tout le fichier et reprendre la main dans l'interpréteur.- Lorsque vous évaluez une expression depuis l'interpréteur, il faut faire un premier pas en détaillant l'expression, c'est à dire qu'il faut cliquer une première fois sur "Step". Si vous utilisez "Go", il donnera directement le résultat, sans détailler l'évaluation de l'expression.
On regarde la fonction compte_triangle, qui utilise une boucle pour calculer la somme 1+2+3+...+n:
def compte_triangle(n): """calcule le n-ème nombre triangulaire, en utilisant une boucle""" r = 0 for i in range(1, n+1): r = r+i return r
Activez le débogueur et évaluez l'expression compte_triangle(15). Vérifiez les choses suivantes :
- l'argument de la fonction est bien une variable locale et a la valeur attendue,
- les autres variables locales n'apparaissent que lorsqu'on les définit,
- le compteur de boucle est bien initialisé à la première valeur du
range(...), - le compteur de boucle est automatiquement mis à sa valeur suivante lors d'un nouveau passage dans la boucle.
Utilisez le débogueur pour répondre aux questions suivantes :
- après le dernier passage dans une boucle
for i in range(debut, fin, 1), est-ce que la variableiprend la valeurfin? - à la fin d'une boucle, est-ce que la variable locale servant de compteur de boucle disparait ?
Nous utiliserons maintenant le code suivant, qui permet de compter combien de "6" ont étés obtenus lors de n lancers d'un dé à 6 faces : (vous pouvez faire un copier/coller ou télécharger le fichier exemple-tp3.py contenant cette fonction et la suivante).
from random import randint def compte_6(n): """compte combien de "6" sont obtenus lors de n tirages aléatoires entre 1 et 6.""" compteur = 0 for i in range(0, n, 1): resultat = randint(1, 6) # tirage aléatoire d'un nombre entre 1 et 6 if resultat == "6": compteur = compteur + 1 return compteur
La première ligne nous permettra d'utiliser la fonction randint(a,b) qui permet d'obtenir un nombre entier aléatoire entre a et b.
- Désactivez le débogueur et évaluez, dans l'interpréteur, l'expression
compte_6(600). Quel est le résultat attendu ? Quel est le résultat constaté ? - Réactivez le débogueur (en cochant la case "Source" et décochant la case "Stack") et relancez l'évaluation de l'expression
compte_6(600). Utilisez le mode pas à pas :- appuyez une fois sur la touche "Step" pour commencer l'appel détaillé à la fonction
compte_6, - appuyez ensuite sur la touche "Over" pour détailler les calculs successifs sur chaque ligne.
- appuyez une fois sur la touche "Step" pour commencer l'appel détaillé à la fonction
- Vérifiez ce qui se passe lorsque le résultat du tirage aléatoire est un
6et, lorsque vous avez trouvé l'erreur, appuyez sur la touche "Go" pour finir l'exécution. - Corrigez le bogue.
Activez le débogueur et lancez l'évaluation de l'expression compte_6(35).
- Vérifiez que le bouton "Step" permet de détailler toutes les étapes de calcul :
- la première fois, cela permet de rentrer dans la fonction
compte_6, - lorsqu'une ligne contient un appel à la fonction
randint, le débogueur détaille le calcul de la fonctionrandint, en ouvrant le code de cette fonction dans une nouvelle fenêtre,
- la première fois, cela permet de rentrer dans la fonction
- Vérifiez que le bouton "Out" permet de terminer l'évaluation de la fonction actuelle sans détails : lorsque que le débogueur est en train de détailler un appel à la fonction
randint, il passe tout de suite à la ligne suivant l'appel en question, dans la fonctioncompte_6, (vous pouvez alors refermer la fenêtre contenant le code de la fonctionrandint) - Vérifiez que le bouton "Over" permet de ne pas détailler les appels à une fonction : lorsqu'une ligne contient un appel à la fonction
randint, le débogueur passe directement à la ligne suivante, - Vérifiez que le bouton "Go" permet de finir le calcul.
Encore des boucles
Écrivez une fonction fact (pour factorielle) avec un argument entier n pour calculer 1 * 2 * 3 * ... * n.
Comme pour la fonction compte_triangle, vous utiliserez un accumulateur pour calculer le résultat final par étapes successives.
Utilisez le débogueur pour vérifier la valeur de l'accumulateur à chaque tour de boucle. Pour n=5, il doit valoir successivement
- 1
- 2
- 6
- 24
- 120 (c'est le résultat)
Mathématiquement, le nombre e est égal à la somme infinie 1 + 1/1! + 1/2! + 1/3! + 1/4! + ...
On peut donc calculer une approximation du nombre e en calculant 1 + 1/1! + 1/2! + 1/3! + 1/4! + ... + 1/n!.
- Écrivez une fonction
approx_eavec un argument entiernpour calculer une telle approximation. - Que pensez vous du calcul
approx_e(100)lorsque votre fonctionfactaffiche des informations ? Commentez la ligne correspondante dans la fonctionfactavant de continuer. - Ajoutez une ligne avec un print (dans la fonction
approx_e) pour afficher les approximations successives, et commentez cette ligne dès que vous avez répondu à la question suivante. - Le nombre e est à peu près égal à 2.71828 18284 59045 23536 02874 71352 66249.... Cherchez la plus petite valeur de n pour que votre fonction trouve correctement les 10 premières décimales de e.
Mathématiquement, le nombre π/4 est égal à la somme infinie 1/1 + -1/3 + 1/5 + -1/7 + 1/9 + ...
On peut donc calculer une approximation du nombre π en calculant 4*(1/1 + -1/3 + 1/5 + -1/7 + ... + (-1)n/(2n+1)).
- Écrivez une fonction
approx_piavec un argument entiernpour calculer une telle approximation. - Ajoutez une ligne avec un print pour afficher les approximations successives, et commentez cette ligne dès que vous avez répondu à la question suivante.
- Le nombre π est à peu près égal à 3.14159 26535 89793 23846 26433 83279 50288.... Cherchez la plus petite valeur de n pour que votre fonction trouve correctement les 5 premières décimales de π.
Retour sur le débogueur: mode automatique et points d'arrêts (facultatif)
Lorsque l'on recherche des bogues, il est parfois utile d'arrêter une fonction à un endroit précis. Pour cela, on peut insérer des points d'arrêt dans le programme. Avec Idle, il suffit de faire un clique droit sur la ligne et de cliquer sur la commande Set Breakpoint. La ligne sera alors surlignée en jaune.
Le bouton "Go" du débogueur permet de continuer l'exécution sans détails, jusqu'au point d'arrêt suivant.
On regardera maintenant le code suivant (vous pouvez faire un copier/coller ou télécharger le fichier exemple-tp3.py contenant cette fonction et la précédente)
from random import randint def compare_lancers(n): """compare les résultats obtenus en tirant 2n fois : - sur les n premiers tirages, en tirant un nombre entre 2 et 12, - sur les n tirages suivant, en tirant deux nombres indépendants entre 1 et 6 et en les additionnant. À chaque fois, les nombres sont ajoutés Le résultat sera la moyenne des tirages pour le type de tirage meilleur. Par exemple, on pourra obtenir (pour n=4) les tirages suivants - 7, 10, 2, 3 pour un total de 22, - 1+3, 2+2, 5+2, 6+4 pour un total de 25. La meilleure moyenne est donc 25/4 soit 6.25.""" resultat1 = 0 # total des tirages avec un nombre entre 2 et 12 for i in range(0, n, 1): nb = randint(2, 12) resultat1 = resultat1 + nb resultat2 = 0 # total des tirages avec deux nombres entre 1 et 6 for j in range(0, n, 1): nb1 = randint(1,6) nb2 = randint(1,6) resultat1 = resultat2 + nb1 + nb2 if resultat1 > resultat2: moyenne = resultat1 / n else: moyenne = resultat2 / n return moyenne
Désactivez le débogueur et évaluez l'expression compare_lancers(1000). Quel est le résultat attendu ? Quel est le résultat obtenu ?
Réactivez le débogueur et insérez un point d'arrêt sur la déclaration de resultat2.
Lancez l'évaluation de compare_lancers(1000) puis :
- commencez l'évaluation en mode pas à pas en regardant l'évolution de la variable
resultat1. - Lorsque que vous avez compris ce qui se passe, appuyez sur la touche "Go", qui permet de « sauter » tous les détails jusqu'au point d'arrêt suivant. Vous pouvez vérifiez que la première boucle s'est effectuée normalement en regardant les valeurs des variables
ietresultat. - Continuez l'évaluation en mode pas à pas en regardant l'évolution de la variable
resultat2. Lorsque que vous avez trouvé le bogue, terminez l'évaluation avec le bouton "Go".
Pourquoi est-il préférable de mettre le point d'arrêt sur la ligne précédent la boucle ? Refaites les mêmes opérations avec le point d'arrêt sur la ligne for j in range(1, n, 0).
Insérez un point d'arrêt sur la ligne contenant le return et lancez l'évaluation de compare_lancers(1000). Arrêtez le débogueur sur la ligne contenant le return et comparez les valeurs des variables resultat1 et resultat2. Quel type de lancers est plus avantageux ?


