Consignes

La note ne valide pas seulement le résultat de votre programme, mais également son style :

Vérifiez ces points avant de demander à votre intervenant de valider votre code.

Liens utiles

Vous aurez également besoin du fichier boulet.py.

Objectifs du TP

Le but de ce TP est de revoir certains concepts vu au premier semestre en insistant sur la qualité du code écrit. Le code fourni suit des règles simples pour rendre le code le plus lisible possible :

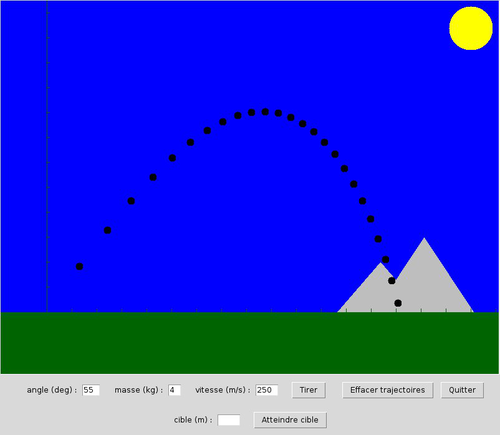
Après quelques exercices préliminaires, nous allons modéliser (et dessiner) la trajectoire d'un boulet de canon en fonction de l'angle de tir, de la vitesse initiale du boulet et de sa masse. Nous chercherons ensuite à ajuster automatiquement l'angle de tir pour essayer d'atteindre une cible précise.

1. Préliminaires : recherche dichotomique et boucle "while"

Le principe de la recherche dichotomique (Wikipedia) est de chercher une solution d'un problème en coupant l'ensemble des solutions possible en deux parties égales à chaque étape. Au bout d'un moment, soit la solution est trouvée, soit l'ensemble devient vide et il n'y a pas de solution.

Par exemple, pour trouver un nombre entre 0 et 100 par questions oui/non successives, les stratégies suivantes ne sont pas très efficaces : on pose les questions

jusqu'à obtenir la réponse oui. Il faut poser 50 questions en moyenne et, au pire, il faudra en poser 100 !

La strategie optimale est de séparer l'ensemble des nombre en 2 parties égales (ou presque) à chaque question. On peut poser par exemple :

Si on représente les questions sur un dessin, on a :

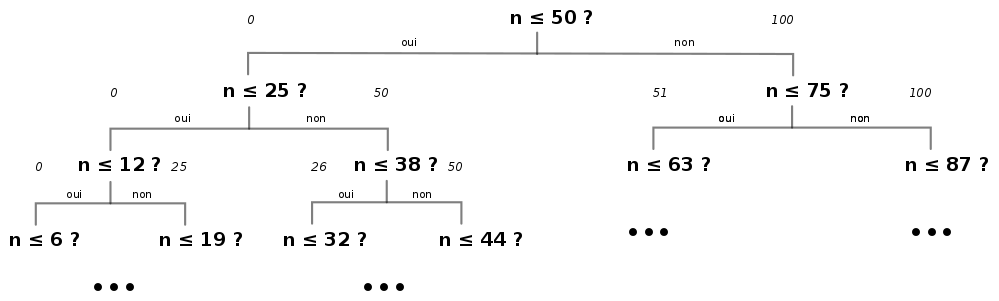Avec cette stratégie, il ne faudra jamais plus de 7 questions pour arriver à trouver le nombre !

Le principe est le suivant : pour chercher un nombre entre a et b, on demande s'il est inférieur ou égal a à m, où m est la moyenne de a et b. Si la réponse est oui, on recommence à chercher entre a et m, et si la réponse est non, on recommence à chercher entre m+1 et b.

Dans tous les cas, on ne connait pas à l'avance le nombre de question à poser. La boucle "while" est donc plus appropriée.

La procédure suivante implante la stratégie naïve qui teste tous les nombres jusqu'à tomber sur le nombre choisi par l'utilisateur : 

def strategie_naive():
    """implémentation de la stratégie naïve qui cherche un nombre entre
    et 100 choisi par l'utilisateur.
    """

    print("Pense à un nombre entre 0 et 100 puis appuie sur 'Enter'...")
    input()

    trouve = False	# variable qui passe à vrai quand on a trouvé le nombre
    nb_questions = 0

    nb = 0	# nombre deviné : on va tester tous les entiers de 0 à 100
    while not trouve:
        # on demande si le nombre est égal à nb :
        question = "Est-ce que ton nombre est égal à " + str(nb) + " ? [o/n]  "

        reponse = ""
        while reponse not in ["o", "n"]:
            reponse = input(question)

        if reponse == "o":
            print("oui !")
            trouve = True   # pour arrêter la boucle
        elif reponse == "n":
            print("non...")
            nb = nb + 1	    # pour passer au nombre suivant

        nb_questions = nb_questions+1

    print("Ton nombre est égal à", nb,
          "et il m'a fallu", nb_questions, "questions pour le trouver.")
  1. Copiez ce programme dans un fichier,
  2. testez la fonction strategie_naive(),
  3. lisez le code de la fonction pour comprendre comment elle fonctionne,
  4. modifiez la fonction pour qu'elle utilise une recherche dichotomique.

Combien de questions sont nécessaires pour trouver un nombre entre 1 et 100 ? Entre 1 et 1000 ? Entre 1 et 10000 ?

2. Le boulet de canon...

2.1. Modélisation de la trajectoire

La trajectoire d'un objet inerte est régie par les lois de la mécanique. Nous allons utiliser une approximation de ces lois pour modéliser de manière discrète la trajectoire d'un boulet de canon.

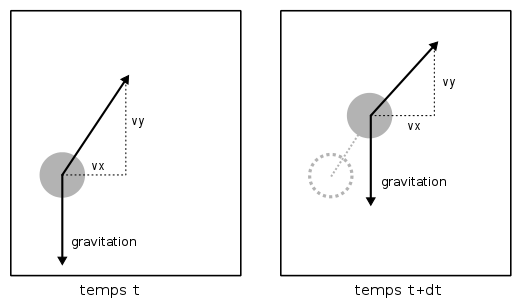
À un instant t donné, le boulet a

et il est soumis à la force d'attraction terrestre. Au temps t + dt, la position et la vitesse du boulet sont modifiées en utilisant les valeurs précédentes :

Attention : dans ces formules, la différence de temps dt est exprimé en secondes.

Pour que la modélisation ressemble à la réalité physique, il faut que dt soit assez petit.

Écrivez une fonction "trajectoire_boulet" qui prend en argument les valeurs suivantes :

La valeur de retour de la fonction est la distance parcourue par le boulet avant qu'il touche le sol. (Il s'agit donc de la dernière valeur de x.)

Votre fonction devra afficher (en utilisant la procédure dessine_boulet(x,y)) le boulet aux positions intermédiaires appropriées (argument freq).

Vous devez écrire votre fonction dans le fichier à trous suivant : boulet.py.

  1. Le fichier fourni comporte une ligne 

    from math import sin,cos,pi
    Vous pouvez donc utiliser les fonctions sinus et cosinus, ainsi que la constante π. Attention, les fonctions trigonométriques de Python utilisent des angles en radians, alors que votre fonction utilise un angle en degrés...
  2. Pour tester votre fonction, il suffit de lancer Python sur le fichier (menu "Run" -> "Run Module F5") et d'utiliser la petite interface.

2.2. Recherche dichotomique de l'angle pour atteindre une cible

Nous cherchons maintenant à atteindre une cible, avec une précision de 1 mètre. Pour ceci, il faudra tirer des boulets (avec la fonction trajectoire_boulet) et modifier l'angle en fonction de la distance parcourue par le boulet : on commence par tirer un boulet à 45°, puis,

Écrivez la fonction dichotomie, qui prend en argument :

Votre fonction appellera la fonction précédente trajectoire pour calculer et afficher les trajectoires du boulet.

2.3. Distance maximale (bonus)

(Bonus)

L'angle de 45° permet d'envoyer un boulet le plus loin possible seulement lorsque la résistance de l'air n'est pas prise en compte. Comme on utilise des formules qui modélisent la résistance de l'air, l'angle permettant d'obtenir une distance maximale est en fait plus petit que 45°, et il dépend des paramètres comme le poids ou la vitesse du boulet.

Écrivez une fonction 

def distance_max(masse, vitesse, dt, freq):
    """Cette fonction doit calculer l'angle approprié pour envoyer un boulet
le plus loin possible.
    - masse : masse du boulet de canon,
    - vitesse : vitesse initiale du boulet canon, en mètre / seconde
    - dt : intervalle de temps  utilisé pour les calculs (en centièmes de
      secondes),
    - freq : fréquence des positions à afficher lors des appels à la fonction
      trajectoire_boulet.
La fonction renvoie la valeur de l'angle trouvé...
"""

La méthode optimale pour une telle recherche est similaire à la recherche dichotomique, mais pour chercher le maximum entre a et b, on calcule

Il y a maintenant 3 cas :

  1. Si la première valeur est strictement plus grande que la seconde, le maximum ne peut pas être dans le dernier tiers. On recommence à chercher entre a et b - (b-a)/3.
  2. Si la première valeur est strictement plus petite que la seconde, le maximum ne peut pas être dans le premier tiers. On recommence à chercher entre a+(b-a)/3 et b.
  3. Si la première valeur est égale à la seconde, le maximum est forcément dans le tiers du milieu. On recommence à chercher entre a+(b-a)/3 et b-(b-a)/3.

On parle parfois de recherche ternaire.

(Note : le dernier cas peut en fait être ignoré : il suffit de remplacer "strictement plus petite" par "plus petite ou égale" dans le deuxième cas. Cela ne change pas vraiment le nombre d'opérations pour trouver le maximum.)