Consignes
Le rendu de TP se fera uniquement à travers l'interface web TPLab. Vous devrez fournir un unique fichier prenom-nom.c contenant votre programme, ainsi qu'un fichier `rc4.c` pour la question 1.
Attention, le seul fait que votre programme fonctionne ne suffit pas pour avoir une bonne note. Les points suivants seront pris en compte :
-
l'architecture de votre programme (code découpé en fonctions etc.),
-
la lisibilité de votre programme (choix pertinent pour les noms de variables etc.),
-
la présence de commentaires aux endroits appropriés,
-
la présence de documentation pour vos fonctions.
Attention, les points suivants ne rapportent rien, mais ne pas les respecter pourra retrancher jusqu'à 10 points sur la note finale :
-
chaque fichier devra comporter un commentaire au début avec vos nom, prénom, filière et numéro du TP,
-
votre code doit compiler avec les options -Wall -Werror -Wextra -pedantic -std=gnu99 -O3,
-
une exécution du programme principal « à vide » (./craque) ne devra pas provoquer d'erreur.
Liens utiles
1. Chiffrement avec RC4
« RC4 » peut-être vu comme un générateur pseudo-aléatoire qui permet de chiffrer un flot de données sur le modèle du « bloc-notes à usage unique » : chaque octet du flot de données est combiné (avec un XOR) avec l'octet correspondant de RC4. On ne connait pas, à ce jours, d'attaque générale pour RC4. (Voir https://en.wikipedia.org/wiki/RC4#Security pour des détails sur d'autres attaques.)
RC4 comporte deux phases :
-
initialisation à partir d'une clé de taille 0 ≤ t ≤ 256 octets (le "key scheduling algorithm"),
-
génération d'octets aléatoires (le "pseudo random generator algorithm").
En pseudo C, si on note cle la clé, et t sa taille
:
/* KSA: Key Scheduling Algorithm */
/* L'état est constitué des variables P (tableau de 256 octets), index_i et index_j (entiers). */
for(i = 0; i < 256; i++)
P[i] = i;
j = 0;
for(i = 0; i < 256; i++) {
j = (j + P[i] + cle[i % t]) % 256;
P[i] <-> P[j]; /* échange */
}
index_i = 0;
index_j = 0;
et
/* PRGA: Pseudo Random Generator Algorithm */
index_i = (index_i + 1) % 256;
index_j = (index_j + P[index_i]) % 256;
P[index_i] <-> P[index_j]; /* échange */
octet_aleatoire = P[ (P[index_i] + P[index_j]) % 256];
Le PRGA est exécuté autant de fois qu'il faut d'octets aléatoire...
Programmez une fonction
void code_RC4(byte* Cle, int taille_cle, byte* Message, int taille_message, int n);
qui chiffre la chaine message avec la clé cle et
affiche le résultat en hexadécimal (format %02X pour
printf) sur la sortie standard.
L'argument n sera le nombre d'octets initiaux non utilisés lors
de la génération. (Autrement dit, on attend n octets générés
avant de commencer à chiffrer.) On appelle parfois ce générateur
RC4-drop[n].
-
Le type
byteest défini partypedef unsigned char byte;pour définir un type pour les octets (entiers entre 0 et 255).
-
Ma fonction principale est
int main(int argc, char* argv[]) { if (argc != 4) { printf("RC4-drop[n], utilisation : %s cle message n\n", argv[0]); exit(-1); } code_RC4((byte*)argv[1], strlen(argv[1]), (byte*)argv[2], strlen(argv[2]), atoi(argv[3])); return 0; }Elle permet d'appeler la fonction
code_RC4_dropdirectement à partir de la ligne de commande :$ ./rc4_drop-n cle message 17 La clé est "cle" et le message clair est "message" Les 17 premières étapes seront ignorées. Le code obtenu est : 484EB4A859834E -
Pour tester : vous pouvez utiliser le tableau suivant. L'argument
Kcorrespond à la colonne "clé", l'argumentMà la colonne "texte clair" et l'argumentnprend la valeur 0. Le résultat codé doit être égal à la colonne "texte chiffré".clé octets générés texte clair texte chiffré Key EB9F7781B734CA72A719... Plaintext BBF316E8D940AF0AD3 Wiki 6044DB6D41B7... pedia 1021BF0420 Secret 04D46B053CA87B59... Attack at dawn 45A01F645FC35B383552544B9BF5 Un exemple avec une valeur de
n=123:clé texte clair ntexte chiffré lorem ipsum 123 4FC201FAFF
2. WEP et RC4
Pour récupérer l'archive contenant les fichiers pour la suite du TP,
remplacez tp3.html dans l'url du TP par
TP-WEP/tp3-XXXXXXXXXXXXXX.tar, où XXXXXXXXXXXXXX est le codage RC4 de "info607" en utilisant la clé "WEP" et en jetant les 1234 premiers octets du
générateur pseudo-aléatoire. (Argument n à 1234 donc.)
Attention, les chiffres hexadécimaux sont en majuscules
(printf("%02X",o)).
L'archive du TP contient un répertoire info607-TP3 qui contient les fichiers :
-
Makefile : n'oubliez pas de changer la variable NOM
-
genere_WEP.c le générateur RC4 simulant des paquets WEP,
-
severus-snape.c un fichier squelette que vous devrez compléter.
Introduction
Le WEP ("Wired Equivalent Privacy") chiffre chaque paquet en utilisant deux clés :
-
la clé WEP, sur 40 ou 104 bits, càd sur 5 ou 13 octets,
-
une "clé" temporaire, ou vecteur d'initialisation sur 24 bits, càd sur 3 octets.
Chaque paquet est codé avec RC4 en utilisant la concaténation "vecteur d'initialisation @ clé WEP" (sur 8 ou 16 octets donc) comme clé. Le vecteur d'initialisation est envoyé en clair avec le paquet chiffré.
Pour décoder, on récupère le vecteur d'initialisation, concatène la clé WEP derrière et décode avec RC4.
De cette manière, on ne peut décoder que si on possède la clé WEP, et on utilise quand même des clés (en général) différentes pour chaque paquet. (C'est important, car sinon, il suffirait d'un paquet décodé pour retrouver le début de la suite pseudo-aléatoire, et donc de pouvoir décoder tous les paquets de taille inférieure.)
2.1. Générateur de paquets WEP
Pour éviter d'avoir à récupérer des paquets réseaux, nous allons générer l'information nécessaire pour l'attaque (et seulement cette information) avec un programme spécifique (fourni). Ce programme génèrera une séquence de
-
un vecteur d'initialisation
-
les 2 octets générés par RC4 avec la clé complète.
Ces informations sont disponibles dans chaque WEP. (Voir plus haut.) Notez que l'attaque n'a besoin que du premier octet généré par RC4 (ou parfois des 2 premiers).
La clé WEP utilisée pourra être choisie au lancement du générateur, ou bien être tirée aléatoirement.
Ce code est contenu dans le fichier generate_WEP.c, qui est compilé automatiquement par le fichier Makefile fourni.
$ make
gcc -Wall -Wextra -pedantic -std=gnu99 -O3 -Wno-unused-variable generate_WEP.c -o generate
...Pour l'utiliser, les options sont les suivantes :
$ ./generate -h
Usage : ./generate [options]
--key_size=<N>, -l<N>
taille en octets de la clé WEP aléatoire (défaut : 13)
--IV_size=<N>, -i<N>
taille en octets des vecteurs d'initialisation (défaut : 3)
--key="<KEY>", -K"KEY"
utilise la clé donnée en argument sous la forme
".. .. .. .." (en hexadécimal)
--easy, -e
utilise les vecteurs d'initialisation (n+3, 255, ...)
(implique une taille d'IV de 3)
--tube=<FILENAME>, -t<FILENAME>
spécifie le nom du tube à utiliser (défaut: data_WEP)
--increment, -I
les vecteurs d'initialisations sont simplement incrémentés
--show_key, -s
affiche la clé utilisée
--help, -h
affiche ce messageLorsque le générateur est lancé, il est possible de lui demander d'afficher la clé WEP qu'il utilise en lui envoyant le signal SIGUSR1. La ligne de commande correspondante est affiché par le générateur au lancement.
Format des données générées
Le programme generate crée un "tube" (fichier spécial) appelé data_WEP et le remplit avec des paquets d'octets. Chaque paquet est constitué de plusieurs parties :
-
les octets du vecteur d'initialisation (il y en a
IV_size), -
les 2 premiers octets générés par RC4 avec ce vecteur d'initialisation et la clé WEP cherchée,
-
un octet
0x00pour marquer la fin du paquet.
Votre programme devra essayer de retrouver la clé en récupérant des paquets d'octets dans ce tube.
La fonction principale du fichier severus-snape.c ouvre ce tube avec l'appel système
open et stocke le descripteur de fichier correspondant dans une
variable globale tube_fd. Vous pouvez donc y lire des données
avec l'appel système read. Vous pouvez consulter la page de
manuel (man 2 read) pour l'utilisation de cet
appel système.
Pour pouvoir utiliser les paquets générés et stockés dans le tube il est impératif que le générateur soit en cours d'exécution. Le plus simple est de le lancer depuis un autre terminal.
Vous pouvez stopper le générateur avec "Control-c" (dans le shell qui a permis de le lancer), ou bien avec
$ killall generatedepuis n'importe quel autre shell.
Attention, il ne faut avoir qu'un seul générateur en exécution à un instant donné.
Écrivez la fonction (dans le fichier severus-snape.c, pertinemment renommé)
int get_data(byte *IV, byte *o1, byte *o2);
Cette fonction devra
-
lire les octets du prochain vecteur d'initialisation dans
tube_fd(variable globale) pour les mettre dans le tableauIV(de tailleIV_size, variable globale), -
lire les octets générés correspondant et le mettre dans
o1eto2, -
lire l'octet suivant et vérifier qu'il s'agit bien d'un
0x00.
Si tout fonctionne, votre fonction renverra la valeur de
IV_size. Sinon, elle renverra un nombre strictement négatif.
Pour tester, vous pouvez passer par la fonction perform_tests
(dans le fichier tests-severus-snape.c,
pertinemment renommé). Cette fonction est appelée lorsque vous donnez l'option
-T sur la ligne de commande. Par exemple :
$ killall generate
$ ./generate --increment --key="01 02 03 04 05 06 07 08 09 0a 0b 0c 0d"
clé utilisée: 01 02 03 04 05 06 07 08 09 0a 0b 0c 0d
Pour afficher la clé, vous pouvez utiliser la commande
$ kill -s SIGUSR1 32508et dans un autre shell
$ ./crack -T 8
QUELQUES TESTS
==============
fonction get_data
-----------------
affichage des 8 premiers paquets :
paquet 1 : 00 00 01 => 6d 0f
paquet 2 : 00 00 02 => 05 34
paquet 3 : 00 00 03 => df ef
paquet 4 : 00 00 04 => 5c e2
paquet 5 : 00 00 05 => 45 5c
paquet 6 : 00 00 06 => 88 cd
paquet 7 : 00 00 07 => 15 42
paquet 8 : 00 00 08 => 04 13
Les options du générateur permettent de choisir la clé (01 02 03 04 05
06 07 08 09 0a 0b 0c 0d) et imposent que les vecteurs d'initialisation
soient choisis dans l'ordre 00 00 01, 00 00 02,
00 00 03, etc.
La fonction de test fournie affiche simplement les N premiers paquets contenus dans le tube.
Comme rien n'est choisi aléatoirement, vous devriez obtenir le même résultat...
2.2. Attaque de Fluhrer, Mantin et Shamir
En 2001, Fluhrer, Mantin et Shamir ont montré que l'utilisation de RC4 pour WEP rendait la clé facilement craquable. Il suffit de récupérer un nombre raisonnable de paquets chiffrés.
Le principe général (vu en cours) est le suivant.
-
On récupère des paquets chiffrés avec leurs vecteur d'initialisation (envoyé en clair).
-
Le premier octet de chaque paquet est le "SNAP header" (subnetwork access protocol) qui vaut
0xaapour le WEP. On peut donc en déduire le premier octet généré par RC4 avec la clé constituée du vecteur d'initialisation (connu) et la clé WEP (inconnue). -
Lorsque certaines conditions sont vérifiées, on fait une prédiction sur le premier octet de la clé secrète en utilisant le vecteur d'initialisation et le premier octet généré.
Lorsque suffisamment de prédictions ont été faites, on observera un biais : une valeur est prédite plus souvent que les autres. Ça sera le premier octet de la clé secrète.
On peut recommencer, avec un octet connu supplémentaire : les 3 octets des vecteurs d'initialisation et un octet de la clé secrète.
Détails de l'attaque :
Si on connait n (avec n>0) octets d'une clé RC4
et le premier octet o généré par la clé complète correspondante,
on peut essayer de faire une prédiction sur l'octet numéro n de
la clé :
-
on effectue les
npremières étapes du KSA, -
on vérifie si les 2 conditions suivantes sont vraies :
-
P[1] < n -
P[1] + P[P[1]] == n
-
-
Si oui, on dit que le vecteur d'initialisation est faible et on prédit le nouvel octet (numéro
n) avecprediction = Pi[o] - j - P[n], oùPi[o]est la position deodans la permutationP. (Attention, il ne faut pas oublier de faire un modulo 256 et de garantir que la prédiction est positive.)Si non, on abandonne la prédiction courante.
La fonction crack-WEP (définie dans la suite) gardera la
prédiction qui apparait le plus souvent. Elle cherchera ensuite l'octet
n+1 de la même manière, jusqu'à avoir deviné tous les octets de
la clé WEP.
Pour trouver une clé WEP, la valeur de n sera toujours de la
forme IV_size+k : en effet, on connait toujours les
3 premiers octets de la clé (ce sont les octets du vecteur
d'initialisation) et on cherche les suivants (qui constituent la clé WEP). Le
fait que le vecteur d'initialisation change à chaque fois n'a pas
d'importance.
Le code fournit (fichier severus-snape.c) utilise des variables globales que vous ne devrez pas modifier. Leurs valeurs sont choisies en donnant des options sur la ligne de commande. Les plus importantes sont :
-
key_sizepour la taille des clés WEP utilisées (5 ou 13, mais votre code devra fonctionner avec d'autres valeurs), -
IV_sizepour la taille des vecteurs d'initialisation utilisés (3, mais votre code devra fonctionner avec d'autres valeurs).
Vecteurs faibles
Écrivez la fonction suivante (voir détails de l'attaque)
int weak(int n, byte *key, byte o1, byte o2, byte *prediction);
qui teste si le vecteur d'initialisation (contenu dans les premiers octets de
key) est faible.
-
L'argument
ndonne le nombre d'octets de la clé déjà connus (en comptant les octets du vecteur d'initialisation), -
l'argument
keycontient le vecteur d'initialisation courant (dans les premières cases) puis les octets connus de la clé, (le contenu des cases suivantes n'est pas spécifié) -
l'argument
oest le premier octet généré par RC4 avec la clé complète (inconnue). (Attention, il ne faut pas faire le XOR avec0xaa. Cette opération est faite implicitement par le processus generate.) -
l'argument
predictionsert renvoyer la prédiction correspondant à ce vecteur d'initialisation (lorsqu'il est faible).
La fonction devra renvoyer 1 lorsque le vecteur d'initialisation
est faible et 0 lorsqu'il n'est pas faible.
-
Dans cette version de
weak, l'argumento2n'est pas utilisé. -
Vous pouvez commencer par tester votre fonction en regardant uniquement si le vecteur est faible, sans faire la prédiction. Si cela fonctionne, vous pourrez alors passer au calcul de la prédiction.
Voici quelques exemples :
nkeyofaible prediction3 {0x53, 0x7a, 0xad}0x2bnon - 4 {0x5a, 0xa4, 0xcb, 0x01}0xd7non - 6 {0xd8, 0x77, 0x9e, 0x01, 0x02, 0x03}0xfanon - 7 {0x78, 0x89, 0xec, 0x01, 0x02, 0x03, 0x04}0x21oui 0x0f8 {0x82, 0x7f, 0xe2, 0x01, 0x02, 0x03, 0x04, 0x05}0x83oui 0x6e10 {0xf8, 0x0b, 0xe2, 0x01, 0x02, 0x03, 0x04, 0x05, 0x06, 0x07}0x2eoui 0xf912 {0x22, 0xe0, 0xba, 0x01, 0x02, 0x03, 0x04, 0x05, 0x06, 0x07, 0x08, 0x09}0x29oui 0xd614 {0xf7, 0x3b, 0xe1, 0x01, 0x02, 0x03, 0x04, 0x05, 0x06, 0x07, 0x08, 0x09, 0x0a, 0x0b}0x03non - Les octets en italiques correspondent au vecteur d'initialisation contenu dans les premiers octets de la clé.
Attaque sur la clé complète
Écrivez la fonction suivante (voir détails de l'attaque)
int crack_WEP(byte* cle_WEP);
qui permet de deviner tous les octets d'une clé WEP en cherchant des vecteurs d'initialisation faibles.
Vous devrez pour ceci faire plusieurs prédictions pour chaque octet de la clé, et ne garder que la plus fréquente.
Le nombre de prédictions à faire pour chaque octet de la clé dépend des deux
variables expected_weak_IV et expected_IV :
-
expected_IVdonne le nombre total de vecteurs d'initialisation à regarder pour chaque octet, indépendamment du faite qu'ils soient faibles ou pas (valeur par défaut : 6000000), -
expected_weak_IVdonne le nombre de vecteurs faibles à regarder pour chaque octet (valeur par défaut : 200).
Votre fonction arrêtera de faire des prédictions dès qu'une de ces variables est atteinte. Si une des 2 valeurs est négative (ou nulle), il faudra l'ignorer complètement.
La valeur de retour devra être le nombre d'octets de la clé.
N'oubliez pas, d'afficher l'avancement de votre fonction. Vous pouvez par
exemple utiliser la variable globale VERBOSE pour ajuster le
niveau de détails.
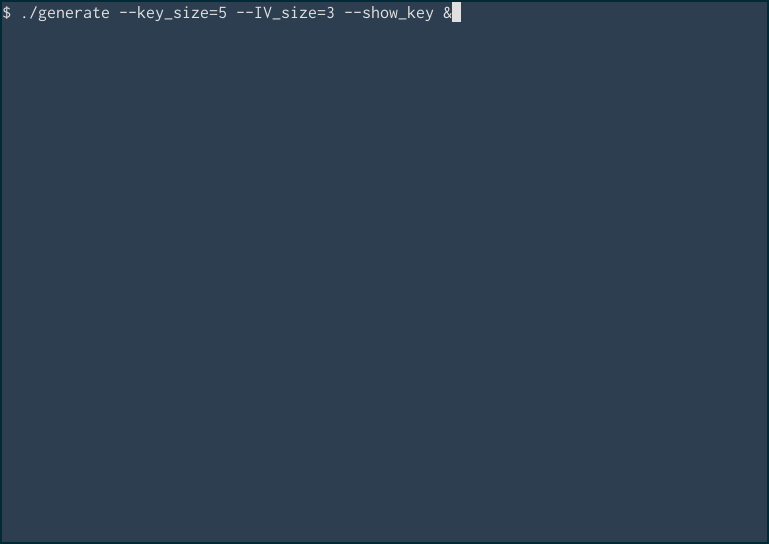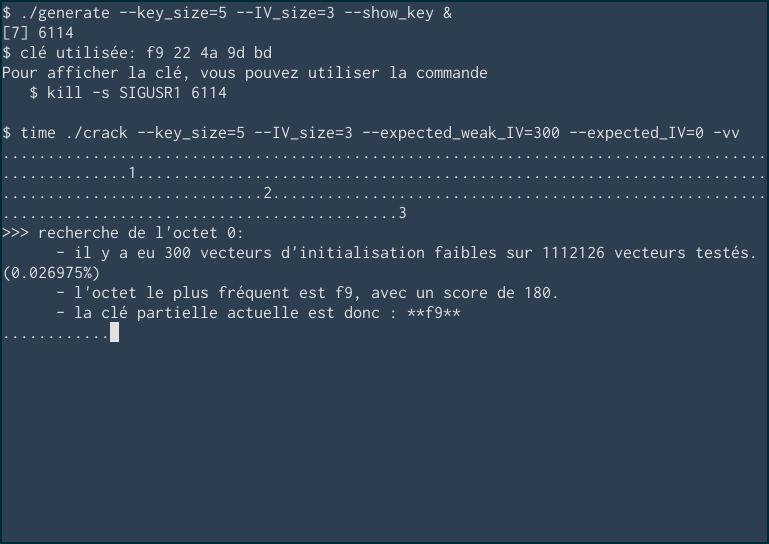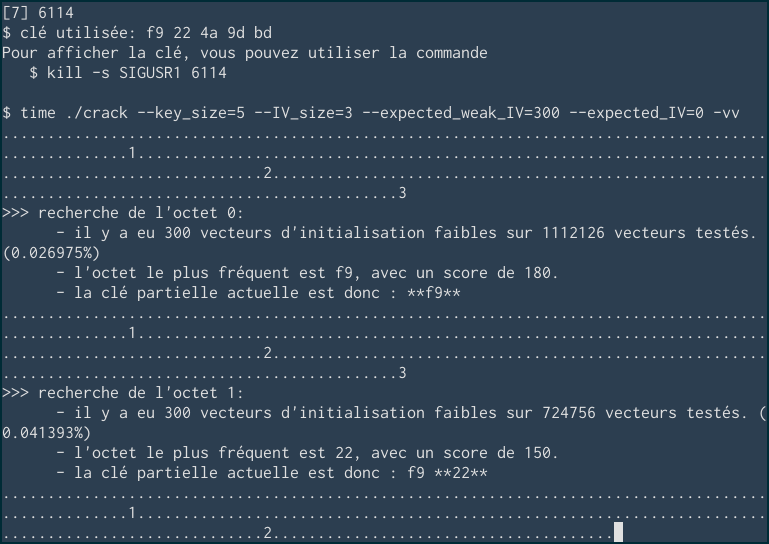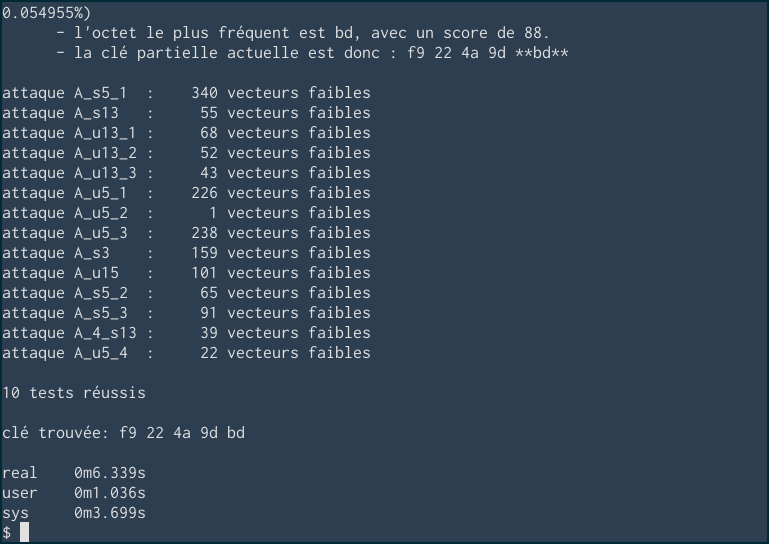
Voici par exemple une exécution de mon programme avec VERBOSE =
2 (option -vv sur la ligne de
commandes). Chaque . affiché correspond à un
vecteur faible trouvé.
Pour vos messages de débogage, la fonction DEBUG s'utilise comme
printf mais avec un premier argument supplémentaire : le niveau
de détails à partir duquel le message est effectivement affiché.
Attention, cle_WEP ne contient que la partie fixe de la
clé alors que la fonction weak prend en argument la clé complète
(partie variable + partie fixe). Il faut donc déclarer une nouvelle variable
pour contenir la clé complète.
Pour vos tests, vous pouvez utiliser l'option --easy du générateur qui permet d'augmenter la proportion de vecteurs faibles générés et accélérer la recherche des clés.
Attention cependant, il n'est pas toujours possible de retrouver la clé dans ce cas.
Vérification
Écrivez la fonction
int check_byte(byte* cle_WEP);
qui récupère un vecteur d'initialisation et les 2 premiers octets générés
(avec la fonction get_data), et vérifie si la clé donnée en
argument génère bien les mêmes octets. La fonction devra renvoyer 1 lorsque
c'est le cas, et 0 sinon.
Vous pouvez réutilisez des morceaux de code que vous avez écrit pour la
question 1. (Attention, la taille de la clé est maintenant égale à
key_size + IV_size.)
Pour tester, vous pouvez choisir la clé utilisée par le générateur avec
l'option --key et définir explicitement la clé
dans votre fonction votre fonction perform_tests:
byte K[] = {0x01, 0x02, 0x03, 0x04, 0x05, 0x06, 0x07, 0x08, 0x09, 0x0a, 0x0b, 0x0c, 0x0d};
if (check_byte(K) == 1) {
...
}
Ajoutez un test à la fin de la fonction crack_WEP qui vérifie si
la clé trouvée génère les même octets que le générateur.
Vous utiliserez pour ceci la fonction check_byte écrite
précédemment et vous testerez nb_tests octets (variable globale
définie par l'option --nb_tests).
-
Si tous les tests réussissent, la fonction
crack_WEPrenverra un nombre strictement positif, -
si aucun test n'est fait (
nb_tests == 0), la fonctioncrack_WEPrenverra0, -
si au moins un test échoue, la fonction renverra un nombre strictement négatif.
Amélioration
L'outils aircrack-ng implémente de nombreuses améliorations à l'attaque de Fluhrer, Mantin et Shamir. Le plus important est de détecter d'autres formes de vecteurs faibles. En voici quelques exemples, avec les prédictions correspondantes :
| attaque | condition | prédiction | taux de réussite |
|---|---|---|---|
| FMS |
P[1]<n et P[1]+P[P[1]]==n
|
Pi[o1]-j-P[n]
|
5% |
| A_s13 |
P[1]==n et o1==n
|
Pi[0]-j-P[n]
|
13% |
| A_u13_1 |
P[1]==n et o1==1-n
|
Pi[o1]-j-P[n]
|
13% |
| A_u13_2 |
P[n]==n et P[1]==0
|
1-j-P[n]
|
13% |
| A_u13_3 |
P[n]==n et P[1]==o1 et P[1]==1-n
|
1-j-P[n]
|
13% |
| A_u5_1 |
P[1]==n (et o1!=1-n et o1!=n) et Pi[o1] < n et Pi[Pi[o1]-n]!=1
|
Pi[Pi[o1]-n]-j-P[n]
|
5% |
| A_u5_2 |
Pi[o1]==2 et P[n]==1
|
1-j-P[n]
|
5% |
| A_u5_3 |
P[n]==n et P[1]>=-n et P[1]==Pi[o1]-n et Pi[o1]!=1
|
1-j-P[n]
|
5% |
Il existe d'autres conditions et prédictions qui utilisent les 2 premiers
octets o1 et o2 générés par RC4 :
| attaque | condition | prédiction | taux de réussite |
|---|---|---|---|
| A_s3 |
P[1]!=2 et P[2]!=0 et P[1]+P[2]<n et P[P[1]+P[2]]+P[2]==n et Pi[o2]!=1 et Pi[o2]!=2 et Pi[o2]!=P[1]+P[2]
|
Pi[o2]-j-P[n]
|
3% |
| A_u15 |
P[2]!=0 et o2==0 et P[n]==0
|
2-j-P[n]
|
15% |
| A_s5_2 |
P[1]>n et P[1] + P[2]==n et o2==P[1] et p!=1 et p!=2 (avec p=Pi[P[1]-P[2]])
|
p-j-P[n]
|
5% |
| A_s5_3 |
P[1]>n et P[1]+P[2]==n et o2!=P[1] et Pi[o2]!=1 et Pi[o2]!=2
|
Pi[o2]-j-P[n]
|
5% |
| A_4_s13 |
n==4 et P[1]==2 et o2==0
|
Pi[0]-j-P[n]
|
13% |
| A_4_u5_4 |
n>4 et P[1]==2 et P[4]+2==n et Pi[o2]!=1 et Pi[o2]!=4
|
Pi[o2]-j-P[n]
|
5% |
(voir les fichiers aircrack-ng.h et aircrack-ng.c)
Implémentez (certaines de) ces améliorations et décrivez comment vous gérez les différents taux de réussite.
Vérifiez expérimentalement, que les prédictions fonctionnent...
Avec toutes ces améliorations, le temps de calcul (et le nombre de paquets à considérer) est environ divisé par 5 !
Attention, le mode --easy n'est plus utilisable lorsque vous ajoutez ces attaques.

