Consignes
Vous devez faire une soumission en fin de première séance !
Vous pourrez ensuite modifier cette soumission jusqu'à la date de la soumission finale.
Le rendu de ce TP se fera uniquement par TPLab et consistera en une archive (zip, tar, etc.) contenant votre code et impérativement un fichier README.
Attention :
-
README doit être un fichier texte contenant les réponses aux questions du TP et vos commentaires / remarques / explications pertinentes, ainsi que le degré d'avancement dans le TP.
-
Votre code doit pouvoir être testé sous Linux sans bibliothèque exotique. N'oubliez pas d'inclure la procédure à suivre pour tester vos programmes, et si vous faites du C / C++, fournissez un fichier Makefile pour la compilation. (N'hésitez pas à vous inspirer de mon fichier Makefile dans ce cas.) Si vous faites autre chose, précisez la procédure d'installation de dépendances / compilation / lancement / etc. dans votre fichier README.
-
Votre programme doit fournir une interface textuelle utilisable. Reportez vous à la section interface pour l'interface de ma version du code. (Vous pouvez vous inspirer de ma fonction
main.) -
Vous devez fournir également une interface pour tester les fonctions intermédiaires. (Notamment pour les questions 1, 2, 3, 5 et 6.) Lisez attentivement les consignes dans la section interface pour éviter de perdre des points inutilement.
-
TPLab refusera les soumissions de plus de 1Mo. Il n'est pas nécessaire de joindre les fichiers de données (tables arc en ciel). Pour info, la taille de mon archive (compressée) fait moins de 10 Ko, et elle fournit plus de fonctionnalités que demandées dans ce TP. (Elle fait moins de 22Ko si j'inclus la seule bibliothèque externe libdivide.)
Tout non respect d'une ou plusieurs de ces consignes entrainera automatiquement un retrait de points sur votre note !
Un point supplémentaire sera supprimé à chaque fois que votre code ne donne pas le résultat attendu sur un des exemples donnés dans le sujet !
Langage de programmation
Le langage de programmation conseillé est C ou C++. Pour vous faire gagner du temps, je vous fournis mon fichier main.c, mon fichier test.c et mon fichier Makefile. Vous pouvez vous en inspirer librement.
Si vous le souhaitez, vous pouvez utiliser un autre langage. (Vérifiez avec l'encadrant que votre choix est raisonnable.) Gardez le point suivant en tête pour votre choix : le programme final (création de tables arc-en-ciel) fait beaucoup de calculs. Les exemples demandés dans le TP restent de taille raisonnable, mais un langage compilé reste de loin préférable.
Pour information, avec ma version du programme (en C), sur l'ordinateur fixe de mon bureau, la création des tables pour la question 14 a pris
-
moins de 1 seconde pour la première table (couverture de 90.18%) ou 4 secondes (couverture de 99.92%),
-
environ 35 secondes pour la seconde (couverture 91.75%) ou environ 6 minutes (couverture 99.89%).
En plus de C ou C++, des étudiants ont fait ce TP en
-
Java : déconseillé car Java n'a pas de type "entier 64 bits non signés". Vous devrez donc utiliser le type
BigIntegerce qui aura un gros impact sur l'efficacité de votre programme. -
Rust
-
Go
Liens utiles
-
encadrant de TP : Pierre.Hyvernat@univ-smb.fr,
-
A Cryptanalytic Time-Memory Trade-Off, l'article original de Martin E. Hellman qui a introduit cette technique,
-
Making a Faster Cryptanalytic Time-Memory Trade-Off, une amélioration par Philippe Oeschslin.
Préliminaires
L'objectif est d'inverser une fonction de hachage H (nous utiliserons SHA1, mais le principe reste le même pour n'importe quelle autre fonction de hachage), c'est à dire, étant donné une empreinte y, de retrouver un x t.q. y = H(x). En pratique, seul l'empreinte des mots de passe est stockée sur un système, et cela permet donc de retrouver un mot de passe à partir de son empreinte.
Fonctions d'empreintes
Voici par exemple comment accéder aux fonctions de hachage standard en C avec la bibliothèque openssl (sudo apt install libssl-dev sous Debian / Ubuntu):
typedef unsigned char byte; // facultatif
#include <openssl/sha.h>
void hash_SHA1(const char* s, byte* empreinte)
{
SHA1((unsigned char*)s, strlen(s), empreinte);
}
N'oubliez pas de lier votre programme avec libcrypto et libssl (-lcrypto -lssl pour gcc / g++) lors de la compilation.
-
Si besoin, installez une bibliothèque (Openssl ou autre) contenant une implémentation de SHA1.
-
Vérifiez que vous savez les utiliser et que vous obtenez les valeurs suivantes :
9F57098C5534762DD32802302DB78ADA1BA864F5 (Salut) DA6645F6E22BF5F75974DC7EED5FCD6160D6B51E (Bob)Attention, les empreintes sont des suites d'octets. Il convient de les afficher convenablement en hexadécimal.
Configuration globale
Notre programme d'inversion sera paramétré par les données suivantes :
-
une chaine
alphabetcontenant les caractères autorisés dans les textes clairs (par exemple"ABCDEFGHIJKLMNOPQRSTUVWXYZ"), -
un entier
tailledonnant le nombre de caractères des textes clairs autorisés, -
un entier
Ndonnant le nombre de textes clairs valides. Ce nombre est calculé à partir de la taille de l'alphabet et detaille.
Définissez une fonction pour calculer N en fonction de
alphabet et taille.
Pour faciliter les améliorations futures, je vous conseille de stocker
alphabet, taille et N dans des
variables globales ou une structure Config globale.
N'oubliez pas de vérifier que la valeur de N est correcte ! Par
exemple :
-
avec
-
alphabet = "abcdefghijklmnopqrstuvwxyz" -
taille = 4
on a
N = 456976(264), -
Interface textuelle
Pour faciliter les tests (les vôtres, et surtout les miens), vous devez fournir une interface facilement scriptable pour appeler toutes les fonctions importantes de votre programme.
Cette interface textuelle doit vous permettre de choisir l'alphabet, la taille des textes clairs, etc.
Voici par exemple l'interface de ma version du programme :
$ ./rbt --help
usage: ./rbt <CMD> [OPTIONS] [ARGS]
Available commands:
create <height> <width> [start] [end] [step] <TEMPLATE>
create the corresponding rainbow tables
info <FILENAME> [LIMIT]
display some information about the table from given file
stats <height> <width> [n] [N]
compute some information about rainbow tables without computing them
(N=number of hash to compute to estimate
time of single hash, default 1000000)
crack <H> <FILENAMES> ...
crack the given hash with the rainbow tables
bruteforce <H>
brute force the given hash
test ...
development tests (run "./rbt test list" for available tests)
Available options:
--alphabet <s> allowed characters for clear text
-A <N> / --abc <N> choose standard alphabet:
N=26 abcdefghijklmnopqrstuvwxyz (default)
N=26A ABCDEFGHIJKLMNOPQRSTUVWXYZ
N=36 abcdefghijklmnopqrstuvwxyz0123456789
N=40 abcdefghijklmnopqrstuvwxyz0123456789,;:$
N=52 ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz
N=62 0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz
N=66 0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz,;:$
-s <n> / --size <n> exact size of clear text (default: 5)
-d <n> / --delay <n> delay (seconds) between log messages (default 5)
-help / -h this messageavec l'interface de mes fonctions de test :
$ ./rbt test list
Available tests:
test config show configuration
test hash <s1> <s2> ... compute hash of strings s1, s2, ...
test c2i <c1> <c2> ... compute c2i(c1), c2i(c2), ...
test i2c <i1> <i2> ... compute i2c(i1), i2c(i2), ...
test h2i <s> <t> [n] compute h2i(H(s), t, n)
test i2i <i1> <t1> ... compute i2i(i1, t1), i2i(i2, t2), ...
test time_i2i [N] compute average time of single i2i call over N calls
test full_chain <width> <i1> ... compute (full) chains starting at i1, i2, ...
test FULL_chain <width> <i1> ... compute (full, with details) chains starting at i1, i2, ...
test chain <w1> <i1> <w2> <i2> ... compute chains starting at i1, i2, ... of length w1, w2, ...
test search <FILENAME> <i> search the first and last occurences of i in table
test list this listEt voila un exemple d'exécution :
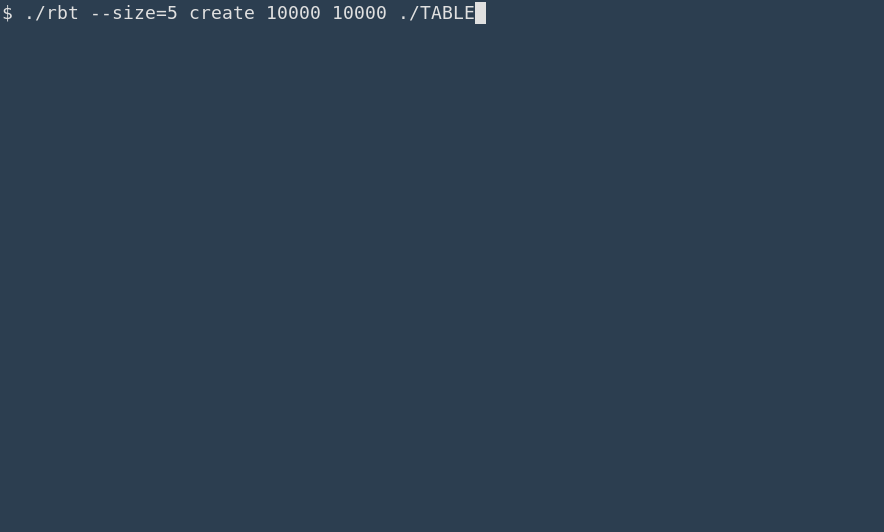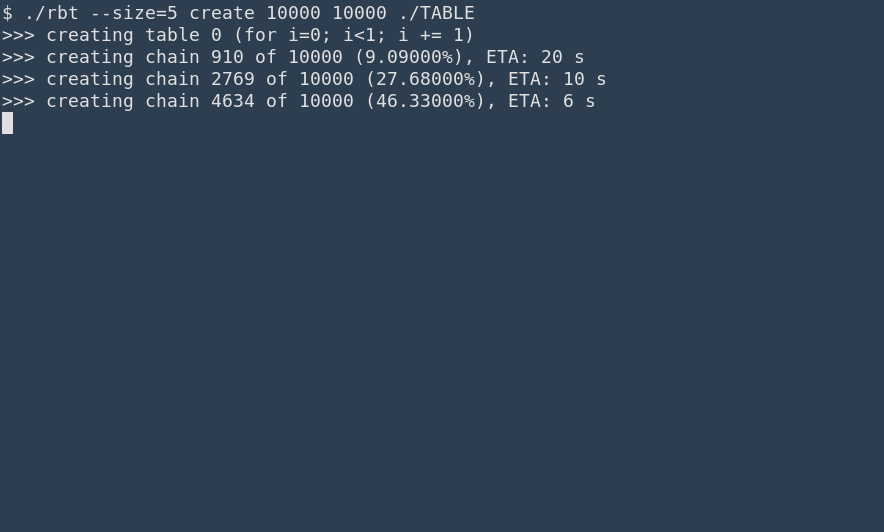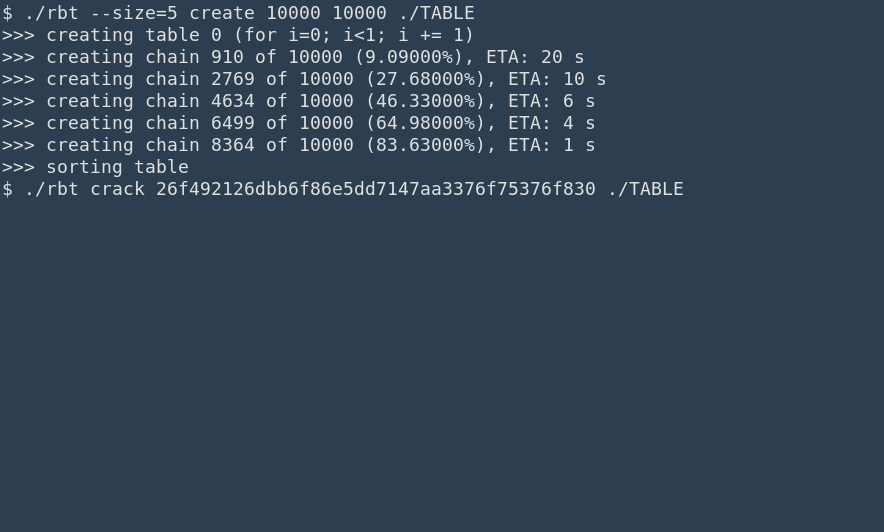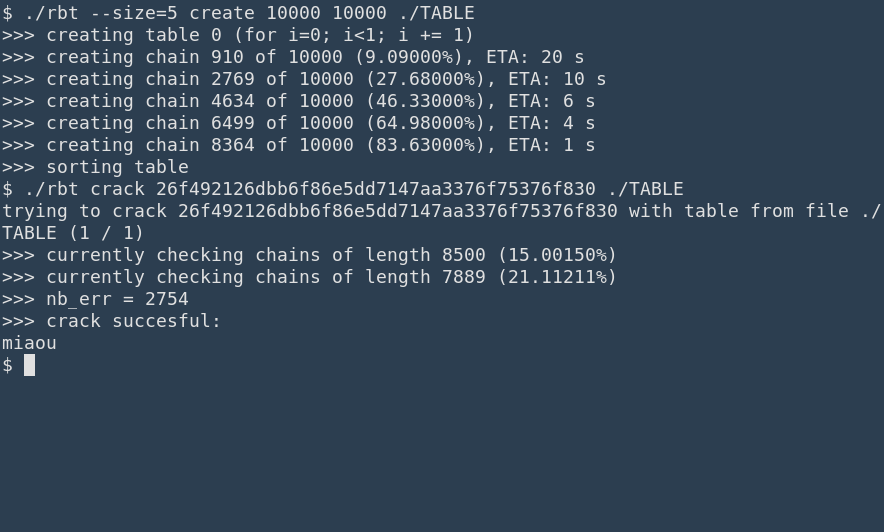
En C / C++, les arguments de la ligne de commande sont passées à la fonction
main dans l'argument argv de type
*char[]. La première chaine argv[0] contient le nom
de l'exécutable, la chaine argv[1] contient le premier argument,
etc. L'argument argc de type int de la fonction
main contient la taille de argv.
En Java, la fonction main accepte un argument String
args[] contenant les arguments, commençant à l'indice 0.
En Python, c'est le tableau sys.argv qui contient les arguments,
commençant à l'indice 1.
Votre fonction main pourra donc contenir quelque chose comme
(C):
if (argc < 2) {
// affiche l'aide
...
exit(1);
}
if (strcmp(argv[1], "test") == 1) {
// commande "test"
...
} else if (strcmp(argv[1], "...") == 1) {
...
}
Traditionnellement, la gestion des arguments de la ligne de commande en C/C++ se fait avec la bibliothèque (standard) getopt pour gérer les options (- suivi d'une lettre, ou -- suivi d'une chaine), éventuellement avec paramètres.
Ajoutez une interface textuelle à votre fonction principale. Vous devrez pouvoir :
-
choisir l'alphabet ainsi que la taille des textes clairs
-
choisir une "commande" :
-
create pour créer une table arc en ciel (question 10),
-
crack pour craquer un mot de passe (question 11),
-
test ... pour lancer des tests. Par exemple, pour les questions précédentes :
./rbt test hash Salut 9F57098C5534762DD32802302DB78ADA1BA864F5 (Salut)et
$ ./rbt --size=6 -A52 test config alphabet = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz" taille = 6 N = 19770609664(Vous pouvez vous inspirer de mon fichier de tests.)
-
etc.
-
Pour le moment, votre interface n'a besoin que des options pour choisir l'alphabet et la taille des mots de passe. Seule les commandes qui permettent de tester les questions 1 et 2 sont nécessaires.
Vous devrez par la suite ajouter les tests et commandes correspondants.
Consignes importantes
Pour ne pas perdre trop de temps, je vous conseille de faire quelque chose de plus simple, au moins dans un premier temps. Par exemple :
$ rbt ALPHABET TAILLE COMMANDE [...]
où argv[1] contient toujours l'alphabet,
argv[2] contient toujours la taille des textes clairs et
argv[3] contient toujours la commande. Les arguments
suivants contiendront les arguments des commandes : texte dont il faut
afficher l'empreinte, taille de la table, nom du fichier, etc.
D'autre part :
-
Affichez un petit message d'aide si aucun argument n'est donné ;
-
affichez un message d'erreur en cas de commande / arguments erronés ;
-
affichez la configuration (alphabet, taille, nombre de textes clairs) dans tous les tests ;
-
associez les tests à des fonctionnalités (ex : ./rbt test i2c 1234567) plutôt qu'à des questions (ex :
./rbt test question_3 1234567) ; -
donnez des exemples de tests faits avec la ligne de commande correspondante dans votre fichier README. Je dois pouvoir refaire des tests similaires et obtenir des résultats cohérents !
Attention, les questions que je ne peux pas tester risquent de ne pas être notées.
Indices et textes clairs
Étant donné un alphabet et une taille , il est
possible de numéroter les textes clairs. Si alphabet =
"ABCDEFGHIJKLMNOPQRSTUVWXYZ", taille = 4, on prend
0 -> AAAA
1 -> AAAB
2 -> AAAC
...
25 -> AAAZ
26 -> AABA
27 -> AABB
...
456974 -> ZZZY
456975 -> ZZZZ # 456976 = 26^4
Le texte clair associé à un nombre est donc sa représentation en base 26. En
particulier, la dernière lettre correspond à n modulo
26.
Programmez la fonction (appelée i2c dans la suite) qui prend un
entier et le transforme en texte clair.
Vérifiez que vous obtenez les valeurs suivantes :
alphabet = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
taille = 4
N = 456976
i2c(1234) = "ABVM"1. Idée du compromis temps-mémoire
Pour commencer, supposons une fonction de hachage H simplifiée : une fonction sur l'ensemble {0, 1, 2,..., N-1}. Étant donné une "empreinte" y (un nombre entre 0 et N-1), on recherche une "entrée" x (un nombre entre 0 et N-1).
- Méthode lente (recherche exhaustive)
-
On teste toutes les entrées possibles et on s'arrête dés qu'on a trouvé x t.q. H(x) = y.
Au pire cas, il faut tester N entrées.
- Méthode "rapide" (précalcul)
-
Si on a précalculé toutes les empreintes et qu'elles sont stockées dans un tableau sous la forme (N = 1000000)
# entrée empreinte 037981 000003 004101 000004 020890 000004 018762 000006 ... 133532 999998 022795 999998Ce (gros) tableau est trié selon la seconde colonne (empreinte).
La fonction H n'est pas forcément injective : il peut donc y avoir des répétitions et des "trous" dans la seconde colonne du tableau.
Pour inverser une valeur, on fait une recherche dichotomique sur y (dans la seconde colonne) pour obtenir directement x t.q. y = H(x).
Par rapport à la précédente, cette méthode nécessite un précalcul très long et de sauvegarder un tableau de taille N. Par contre, l'inversion est très rapide.
- Méthode intermédiaire (compromis temps-mémoire)
-
Si on précalcule des empreintes "consécutives" (empreinte d'empreinte), on peut obtenir un tableau de la forme
# entrée H(entrée) H(H(entrée)) 450527 884710 000005 090419 808110 000006 160224 535710 000006 ... 876129 619817 999997On sauvegarde alors uniquement les première et dernière colonnes pour obtenir
# entrée H(H(entrée)) 450527 000005 090419 000006 160224 000006 ... 876129 999997On cherche alors x t.q. H(x) = y de la manière suivante
-
on fait une recherche dichotomique de y dans la dernière colonne. Si on le trouve, on obtient x' (dans la première colonne) t.q. y = H(H(x')). On peut donc poser x = H(x') !
-
Si on ne trouve pas, on fait une recherche dichotomique de H(y) dans la dernière colonne. Si on le trouve, on obtient x' (dans la première colonne) t.q. H(y) = H(H(x')). x' est un candidat pour un inverse de y.
On teste si y = H(x') : dans le cas positif, on a trouvé un inverse, dans le cas négatif, on continue la recherche.
Par rapport à la deuxième méthode, celle ci nécessite autant de précalculs, mais stocke un tableau plus petit. Par contre, elle nécessite légèrement plus de calcul lors de chaque recherche.
On peut généraliser cette construction en calculant un tableau (toujours trié selon la dernière colonne)
# e H(e) HH(e) HHH(e) HHHH(e) HHHHH(e) H6(e) H7(e) H8(e) ... 731124 132518 839817 585511 145152 061620 317423 511013 020511 ... 611196 895417 928719 758225 350428 648619 882210 264133 390232 ... 522119 229321 851653 812066 064431 699105 247523 487930 677201 ...On peut alors stocker uniquement les premières et dernières colonnes:
# e H8(e) ... 731124 020511 ... 611196 390232 ... 522119 677201 ...On peut généraliser la méthode de recherche précédente : on diminue l'utilisation de la mémoire en augmentant le temps de calculs.
Dans ce cas, on recherche Hk(y) (pour k = 0,1,2,...) dans la dernière colonne, et lorsqu'on le trouve, on teste le candidat potentiel c = H8-k-1(x) correspondant. Ce candidat vérifie Hk(H(c)) = Hk(y) mais pas forcément H(c)=y.
(Note : la quantité de précalculs ne change pas vraiment...)
-
-
Quelle est la complexité (en temps et en espace) de recherche dans une telle table si la table initiale contenait
hauteurlignes etlargeurcolonnes ? -
Comparez cela avec les complexités (en temps et en espace) de la recherche exhaustive et celle du précalcul complet ?
2. Mise en œuvre concrète : précalcul de la table
2.1. Indices et empreintes
Le compromis temps/mémoire décrit plus haut était basé sur une fonction sur un ensemble {0, 1, ..., N-1}. Nous allons l'adapter en transformant notre fonction de hachage H : TextesClairs → Empreintes en une fonction {0, 1, ..., N-1} → {0, 1, ..., N-1} :
| {0, 1, ..., N-1} → TextesClairs → Empreintes → {0, 1, ..., N-1} |
Les nombres entre 0 et N-1 seront appelés des indices. Il y en autant que les textes clairs valides.
La fonction Empreintes → {0, ..., N-1} sera appelée h2i.
On peut choisir h2i(y) = y % N, mais pour limiter les collisions,
on utilise plutôt h2i(y, t) = (y+t) % N, où t dépend
de la colonne dans laquelle on se trouve.
D'autre part, comme l'empreinte y est un très grand
nombre, on n'utilise en fait que ses 8 premiers octets :
h2i(y, t) = (y[0...7] + t) % N
Programmez la fonction h2i et testez la.
Voici un exemple de valeur obtenue :
fonction de hash = SHA1
alphabet = "abcdefghijklmnopqrstuvwxyz"
taille = 5
N = 11881376
hash("oups") = 428f999c99ab7a0580e9597219736b1725063c64
h2i(hash("oups"), 1) = 5529923
En effet, la suite d'octets [0x42, 0x8f, 0x99, 0x9c, 0x99, 0xab, 0x7a,
0x05] se traduit en l'entier 64 bits 394816593593995074,
dont le modulo 11881376 est 5529922.
-
Si vous obtenez un résultat de
4796221026044967429au lieu de394816593593995074(càd8414277au lieu de5529922après le modulo11881376), c'est que vous avez inversé l'octet de poids faible et l'octet de poids fort. L'octet d'indice 0 est l'octet de poids faible ! (convention little-endian) -
En C/C++, les 8 premiers octets de
y(de typeunsigned char*) peuvent directement être convertis en une valeur de typeuint64_tpar un cast deyenuint64_t*. -
En Java, qui n'a pas de type "entier 64 bits non signé", les 8 premiers octets de
ydevront être converti à la main en une valeur de typeBigInteger.
2.2. Table arc-en-ciel
Chaines d'indices
Dans la version "simple", la table consistait en des chaines x, H(x), HH(x), HHH(x), .... Les chaines seront maintenant de la forme
| indice |
i2c
|
clair |
H
|
empreinte |
h2i(_, 1)
|
indice |
i2c
|
... |
H
|
... |
h2i(_, 2)
|
indice | ...... |
h2i(_, n-1)
|
indice |
| i1 | ↦ | c1 | ↦ | h1 | ↦ | i2 | ↦ | c2 | ↦ | h2 | ↦ | i3 | ...... | ↦ | in |
Si on note i2i la composition de i2c,
H et h2i, les chaines sont de la forme
| indice |
i2i(_, 1)
|
indice |
i2i(_, 2)
|
indice |
i2i(_, 3)
|
indice | ...... |
i2i(_, n-1)
|
indice |
| i1 | ↦ | i2 | ↦ | i3 | ↦ | i4 | ...... | ↦ | in |
Programmez la fonction (à deux arguments) i2i, puis la fonction
nouvelle_chaine(idx1, largeur) qui génère une chaine de taille
largeur.
Attention, la chaine finale ne comporte que son point de départ et son point d'arrivé ! Les valeurs intermédiaires sont oubliées.
fonction de hash = SHA1
alphabet = "abcdefghijklmnopqrstuvwxyz"
taille = 5
N = 11881376
chain of length 1: 1 ... 1
chain of length 10: 1 ... 8601992
chain of length 100: 1 ... 3560808
chain of length 1000: 1 ... 9097363Si vous avez besoin de déboguer votre code, voici la chaine complète de taille 100, et la même avec les calculs intermédiaires. Attention, vous ne devez pas stocker les calculs intermédiaires !
Pour éviter d'allouer constamment des nouveaux tableaux pour les empreintes
que vous calculez (dans la fonction i2i), il est conseillé
d'utiliser des variables globales
-
EMPREINTE -
TEXTE
pour stocker les résultats d'empreintes et de textes "clairs".
Table
Il est difficile de garantir que toutes les valeurs possibles sont présentes dans une table arc-en-ciel. En pratique, il suffit qu'elle recouvre l'ensemble des valeurs le mieux possible. Une table pourra ainsi recouvrir 88.3% ou 97.8% des valeurs...
Le plus simple pour cela est de faire commencer les chaines par des indices choisis aléatoirement.
En quoi est-ce que l'ajout du paramètre t dans la fonction
h2i permet d'augmenter la couverture de la table ?
Programmez la fonction index_aleatoire puis la fonction
creer_table(largeur, hauteur).
Attention, la table finale doit être triée par ordre croissant de la dernière colonne.
Voici un extrait d'une table générée non aléatoirement : au lieu d'un indice aléatoire, la nème chaine commence à l'indice n.
>>> table from TABLE
hash function: SHA1
alphabet: abcdefghijklmnopqrstuvwxyz
alphabet length: 26
size: 5
nb clear texts: 11881376
height = 100 (height of table)
width = 200 (width of table)
table number 0 (n)
content:
000000000: 45 --> 20309
000000001: 89 --> 278375
000000002: 72 --> 305658
000000003: 3 --> 794735
000000004: 11 --> 945074
000000005: 86 --> 956000
000000006: 73 --> 1194663
000000007: 20 --> 1245733
000000008: 48 --> 1259309
000000009: 94 --> 1548989
...
000000090: 30 --> 10626782
000000091: 78 --> 10745826
000000092: 42 --> 10785831
000000093: 83 --> 10879054
000000094: 0 --> 11030364
000000095: 10 --> 11066547
000000096: 40 --> 11179419
000000097: 7 --> 11658227
000000098: 1 --> 11690251
000000099: 47 --> 11797675-
Programmez deux fonctions
sauve_tableetouvre_tablepour sauvegarder / ouvrir des tables dans des fichiers.Le plus simple est de stocker les début/fin de chaque chaine au format ASCII sur des lignes du fichier.
Le plus efficace est de stocker les entiers contenus dans la table consécutivement en binaire dans les octets du fichier.
Vous pouvez choisir la méthode que vous voulez, mais il est conseillé d'ajouter une entête au fichier pour stocker
-
les paramètres (
alphabetettaille), -
la taille de la table (
largeurethauteur).
Vous devez pouvoir créer et sauvegarder une table depuis la ligne de commande, par exemple avec
$ ./rbt <PARAMETRES> create 200 200 fichier_table -
-
Programmez également une fonction
affiche_tablequi permettra d'afficher une partie du contenu d'une table. (Par exemple, les premières et dernières valeurs comme ci dessus...) Cette fonction pourra être appelée depuis la ligne de commande, par exemple avec$ ./rbt info fichier_table
Vérifiez sur vos exemple que les fichiers ont une taille cohérente avec la table qu'ils contiennent.
Par exemple, le fichier contenant la table donnée en exemple dans la question précédente fait 1654 octets : 1600 octets contenants les chaines (point de départ et d'arrivée sur 8 octets chacun) et 54 octets d'entête.
La taille de vos entêtes peut varier, mais pas la tailles des données.
3. Mise en œuvre concrète : recherche dans une table arc-en-ciel
Pour inverser la fonction de hachage H, nous allons en fait
inverser la fonction i2i comme décrit dans la section pertinente. Il y a deux subtilités
supplémentaires :
-
la fonction
i2iprend en paramètre le numéro de colonne -
comme la fonction
h2in'est pas injective, un inverse pouri2ine donne pas forcément un inverse pourH, mais seulement un candidat pour un inverse pourH.
Pour une table arc-en-ciel table, si l'on souhaite trouver
x t.q H(x) = y, on procède comme suit :
-
On cherche en supposant que l'empreinte
yest "moralement" un indice dans la dernière colonne detable.On calcule l'indice
j = h2i(y, n-1). Cette valeur est potentiellement présente dans la dernière colonne detable.Si c'est le cas, on pose
i0l'indice correspondant de la première colonne, et on calcule, en partant dei0, l'indice correspondant à l'avant dernière colonne. Cela nous donne un indiceit.q.i2i(i, n-1) = j, c'est à direh2i(H(i2c(i)), n-1) = h2i(y, n-1).Cela nous donne un candidat
i2c(i)pour un inverse dey. On compare doncH(i2c(i))ety:-
en cas d'égalité, on a trouvé un inverse
-
sinon, on continue la recherche.
-
-
Si aucun candidat correct n'a été trouvé, on cherche en supposant que
yest "moralement" dans l'avant dernière colonne detable.On calcule l'indice
j = i2i(h2i(y, n-2), n-1). Cette valeur est potentiellement dans la dernière colonne detable.Si c'est le cas, on pose
i0l'indice correspondant de la première colonne, et on calcule, en partant dei0, l'indice correspondant à la colonnen-2....
Cela nous donne un candidat
i2c(i)pour un inverse dey....
-
etc.
En pseudo-C, cela ressemble à
// essaie d'inverser l'empreinte h
// - table : table arc-en-ciel
// - hauteur : nombre de chaines dans la table
// - largeur : longueur des chaines
// - h : empreinte à inverser
// - clair : (résultat) texte clair dont l'empreinte est h
int inverse(table, hauteur, largeur, h, *clair) {
int nb_candidats = 0;
for (t = largeur - 1; t > 0; t--) {
idx = h2i(h, t);
for (i = t + 1; i < largeur; i++) {
idx = i2i(idx, i);
}
if (recherche(table, hauteur, idx, &a, &b) > 0) {
for (i = a; i <= b; i++) {
if (verifie_candidat(h, t, table[i][0], clair) == 1) {
return 1;
} else {
nb_candidats++;
}
}
}
}
}
où
// recherche dichotomique dans la table les premières et dernières lignes dont
// la seconde colonne est égale à idx
// - table : table arc-en-ciel
// - hauteur : nombre de chaines dans la table
// - idx : indice à rechercher dans la dernière (deuxième) colonne
// - a et b : (résultats) numéros des premières et dernières lignes dont les
// dernières colonnes sont égale à idx
int recherche(table, hauteur, idx, *a, *b) {
...
}
// vérifie si un candidat est correct
// - h : empreinte à inverser
// - t : numéro de la colonne où a été trouvé le candidat
// - idx : indice candidat (de la colonne t)
// - clair : résultat : contient le texte clair obtenu
int verifie_candidat(h, t, idx, *clair)
{
for (int i = 1; i < t; i++) {
idx = i2i(idx, i);
}
clair = i2c(idx);
h2 = H(clair);
return h2 == h;
}
-
Programmez une fonction de recherche dichotomique (fonction
rechercheci dessus) pour rechercher les premières et dernières lignes dont le point d'arrivée est égale à une valeur.Le plus simple pour ceci est de faire une recherche dichotomique habituelle, puis de parcourir la table (vers le haut et vers le bas) à partir de la valeur trouvée pour trouver l'intervalle complet de valeurs.
-
Programmez ensuite la fonction d'inversion...
Cette fonction pourra être lancée depuis la ligne de commande, par exemple avec
$ ./rbt crack AFED3178E2377DFA3DEF13466219C674 ./fichier_table
Estimez la complexité de la recherche dans une table arc-en-ciel.
Vous pouvez estimer la couverture d'une table en fonction des paramètres
(N, largeur et hauteur) de la manière
suivante :
m = hauteur;
v = 1.0;
for (i = 0; i < largeur; i++) {
v = v * (1 - m / N);
m = N * (1 - exp(-m / N));
}
couverture = 100 * (1-v);
Programmez une fonction qui affiche (en fonction des paramètres d'initialisation et de la hauteur / largeur de la table) :
-
une estimation de la taille (en octets) de la table,
-
une estimation de la couverture de la table.
Cette fonction pourra être appelée depuis la ligne de commande, par exemple avec
$ ./rbt <PARAMETRES> stats 200 200Utilisez votre programme pour générer les tables arc en ciel suivantes, et inverser les empreintes correspondantes :
-
alphabet = "ABCDEFGHIJKLMNOPQRSTUVWXYZ,taille = 4:-
des empreintes que vous calculerez vous même (
"ABCD", etc.) -
16de25af888480da1af57a71855f3e8c515dcb61
-
-
alphabet = "abcdefghijklmnopqrstuvwxyz0123456789,;:$.",taille = 5,-
des empreintes que vous calculerez vous même (
"3.141", etc.) -
dafaa5e15a30ecd52c2d1dc6d1a3d8a0633e67e2
-
Décrivez vos résultats dans votre fichier README :
-
les paramètres choisis,
-
temps de calcul des tables,
-
taille des tables,
-
temps de calcul de l'inverse.
Il y a plusieurs causes d'échec :
-
bug dans votre code ; (si si, ça arrive !)
-
paramètres insuffisants : si votre table est trop petite (en largeur et/ou en hauteur), la couverture sera insuffisante ;
-
pas de chance, l'exemple demandé n'est pas dans votre table (même avec une couverture de 99.8%, certaines valeurs ne sont pas dans la table) ;
-
il a un bug dans l'énoncé. (si si, c'est arrivé !)
Pour le point 2, la question 12 peut vous aider à choisir des paramètres pertinents.
Estimez le temps nécessaire de précalcul ainsi que la taille d'une table
arc-en-ciel pour alphabet =
"abcdefghijklmnopqrstuvwxyz0123456789", taille_min = 8.
Refaites la question 13 en faisant une recherche exhaustive. Combien de temps cela prend-il ?
Estimez le temps nécessaire pour faire une recherche exhaustive pour inverser une valeur avec les paramètres de la question 14.
Expliquez pourquoi l'utilisation de sel pour les mots de passe empêche l'utilisation de tables arc-en-ciel.
4. Pour aller plus loin
4.1. Tailles min et max
Souvent, les textes clairs peuvent avoir plusieurs tailles : entre
taille_min et taille_max. Pour gérer ceci, il
"suffit" de modifier la valeur de N calculée, et la fonction
i2c.
Par exemple, si taille_min = 1 et taille_max = 3,
on prendra les textes clairs dans l'ordre suivant :
0 -> A
1 -> B
...
25 -> Z
26 -> AA
27 -> AB
51 -> AZ
52 -> BA
53 -> BB
...
701 -> ZZ
702 -> AAA
703 -> AAB
...
18277 -> ZZZAutrement dit :
-
pour les nombres entre 0 et 26-1 = 25, le texte clair associé est la lettre correspondante ;
-
pour les nombres entre 26 et 26 + 262 - 1 = 701, on soustrait 26 avant de calculer leur représentation en base 26, sur 2 caractères : 53 -> 53-26 = 27 -> BA
-
etc.
Par exemple, pour trouver le texte correspondant à 12345, on fait les étapes suivantes :
-
12345 >= 26, on soustrait donc 26 pour obtenir 12319
-
12319 >= 26*26, on soustrait donc 26*26 pour obtenir 11643
-
11643 < 26*26*26, on convertit donc 11643 sur 3 lettres :
-
11643%26 = 21 -> V
-
11643/26 = 447 et 447%26 = 5 -> F
-
447/26 = 17 et 18%26 = 18 -> R
-
-
le résultat est donc "RFV".
Voici quelques exemples supplémentaires :
alphabet = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz
taille_min = 1
taille_max = 6
N = 20158268676
i2c(150106454) = "Table"
i2c(75324) = "arc"
i2c(1651) = "en"
i2c(4173921) = "ciel"
La fonction i2c est appelée de très nombreuses fois, il convient
donc de la programmer en évitant les calculs redondants. Pour ceci, votre
fonction d'initialisation (question 2) peut également calculer :
-
la taille d'alphabet,
-
un tableau contenant le nombre de textes clair possibles pour chaque taille. Pour
-
alphabet = "abcdefghijklmnopqrstuvwxyz" -
taille_min = 2 -
taille_max = 4
on aurait
T = [676, 17576, 456976](262 = 676, 263 = 17576 et 264 = 456976). -
4.2. Plusieurs tables
Lorsque les tables sont trop grosses, le nombre de collisions augmente, diminuant ainsi la couverture des textes clairs.
Une possibilité est de créer alors plusieurs tables, numérotées de
0 à n-1. La fonction h2i est modifiée
pour accepter un paramètre supplémentaire :
h2i(y, t, n) = (y[0...7] + t + 65536*n) % NChaque table est stockée dans un fichier, et la recherche se fait séquentiellement dans la liste des fichiers. Le temps de recherche augmente, mais la couverture aussi...
4.3. Dictionnaire
On peut combiner une attaque arc-en-ciel et une attaque par dictionnaire : la
fonction i2c renvoie alors le mot à l'indice n dans le
dictionnaire.
Erreurs fréquentes
D'après J.O. Lachaud, voici quelques erreurs qui reviennent souvent dans votre code :
-
Mauvaise génération aléatoire de l'indice. Attention, il faut générer un nombre entier aléatoire suffisamment grand, genre 64 bits. Par exemple,
random, suivant les architectures ne génère pas forcément un nombre assez grand. Une manière de faire est donc de générer deux nombre aléatoires et de les combiner:unsigned long n1 = rand(); unsigned long n2 = rand(); uint64 n = ( (uint64) n2 ) + ( ( (uint64) n1 ) << 32 ); -
Oubli fréquent de prendre le "modulo
N" pour l'indice aléatoire initial. -
Mauvaise transformation d'indice en texte clair. Il faut bien vérifier sur de petits exemples (petits alphabets) que tout se passe bien.
-
Mauvaise transformation de l'empreinte en indice (
h2i). Le plus simple est d'utiliser les conversions type C qui changent le point de vue sur la mémoire:unsigned char t[16]; // empreinte, un grand nombre de 16 octets (pour MD5) uint64_t* ptr = (uint64_t*) t; // le même tableau, vu comme un tableau d'entiers 64 bits uint64_t i = ptr[0]; // par définition le nombre stocké dans t[0-7].En Java, cette fonction est souvent mal vérifiée, car elle ne peut être écrite aussi simplement.
-
Mauvaise comparaison de chaines (en C, C++ et en Java). Vous comparez très souvent l'adresse des chaines, pas leur valeur. Utilisez
equalsen Java,strcmpen C, oustring::operator==en C++ -
Vérifiez votre nombre de mots
N. -
Vérifiez vos tables : elles doivent être triées selon la deuxième colonne et ne doivent pas contenir trop de répétitions/doublons. Si ce n'est pas le cas, vous avez probablement un problème dans la fonction
i2i. -
Confusion entre chaines C (terminées par
'\0') et chaine C++ avec des conversions dans tous les sens. -
Confusion entre la vision affichable en hexadécimal de l'empreinte (pour MD5, 32 caractères parmi 0123456789abcdef) et l'empreinte elle même (un grand entier sur 16 octets). De fait, souvent la version "affichable" du MD5 est utilisée dans
h2i, alors qu'il faut bien la version chiffrée (le grand entier). -
Mauvais paramètre t passé à
h2i. Il faut bien faire attention à la cohérence de ce paramètre entre la génération de la table et la recherche pour cracker le mot de passe.

