Consignes

La collaboration orale est encouragée, mais le partage de code et le copier/coller (via Discord, github, etc.) n'est pas autorisé et pourra être pénalisé.

Le rendu de ce TP se fera uniquement par TPLab et consistera en une archive (zip, tar, etc.) contenant un répertoire TP1_NOM avec au minimum :

votre fichier maze_NOM.py,
votre fichier obstacle_NOM.py,
un fichier README.txt contenant les réponses aux questions et vos remarques et observations.

Vous pouvez ajouter d'autres fichiers s'ils sont documentés dans votre fichier README.txt.

Vous aurez compris que NOM devra être remplacé par votre nom (ou vos noms en cas de binômes) !

Tous vos fichiers doivent comporter une entête avec votre nom et votre groupe de TP.

Tout non respect d'une ou plusieurs de ces consignes entrainera automatiquement un retrait de points sur votre note !

Liens utiles

Lien vers l'archive du TP TP1_ALAN.tar.gz.

Cette archive contient

des classe pour les graphes en listes d'adjacences, pour les premières parties du TP : graph.py,
code à compléter pour les premières parties : maze_ALAN.py,
des exemples de graphes dans le répertoire graph_examples,
des exemples de labyrinthes pour la partie 3, dans le répertoire maze_examples,
code à compléter pour la dernière partie : obstacles_ALAN.py,
des exemples de labyrinthes pour la dernière partie, dans le répertoire obstacles_examples.

1. Préliminaires : listes d'adjacences

1.1. Représentation des graphes

Nous allons représenter les graphes par leurs listes d'adjacence : un graphe à N sommets, numérotés de 0 à N-1 est donné par un tableau A de taille N. La case A[v] donne la liste des voisins du sommet v.

Par exemple, le graphe suivant

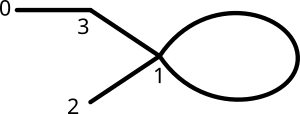
pourra être représenté par

A = [
      [3],              # voisin de 0
      [2, 1, 3],        # voisins de 1
      [1],              # voisin de 2
      [0, 1],           # voisins de 3
    ]

Le fichier graph.py définit une classe Graph qui contient simplement un tel tableau de listes d'adjacence. On peut par exemple initialiser le graphe précédent avec

$ python3
>>> from graph import Graph
>>> G = Graph.empty(4)      # il y a 4 sommets
>>> G[0].append(3)
>>> G[1].extend([2, 1, 3])
>>> G[2].append(1)
>>> G[3].extend([0, 1])
>>> G
([3], [2, 1, 3], [1], [0, 1])

Vous pouvez également lire / écrire un graphe dans un fichier. Par exemple, le graphe précédent se trouve dans le fichier graph1.txt :

# fichier graph1.txt
3
2,1,3
  1
0, 1

et le code suivant permettra de le lire, d'ajouter une arête entre 0 et 2, et sauver le résultat dans un autre fichier.

$ python3
>>> from graph import Graph
>>> G = Graph.from_file("graph1.txt")
>>> G[0].append(2)
>>> G[2].append(0)
>>> G.to_file("graphe-2.txt")

Vous ne pouvez pas ajouter de sommet à un Graph. Il faut l'initialiser avec le bon nombre de sommets.
La seule manière d'ajouter des arêtes est d'utiliser les méthodes G[v].append ou G[v].extend.
Des affectations comme G[v] = [a,b,c] ou G[v] = G[v] + [d,e,f] provoqueront une erreur !
N'oubliez pas que dans un graphe non-orienté, si s1 est dans G[s2], alors s2 doit également être dans G[s1].

Écrivez (dans le fichier maze_ALAN.py) la fonction degre_max qui prend un graphe G en argument et renvoie le degré maximal des sommets du graphe G.

Pour tester cette fonction, complétez la fonction main_test pour qu'elle affiche le degré maximal du graphe. Vous pourrez testez en donnant l'option -T sur la ligne de commande :
```
$ python3 ./maze_ALAN.py -T ./graph_examples/graph1.txt
le graphe contient 4 sommets
degré max du graphe : 3
```

Écrivez également une fonction is_path qui prend en argument un graphe G et une liste de sommets P. Votre fonction devra renvoyer True si les sommets de P (pris dans l'ordre de P) forment un chemin dans G, et False sinon.

Vous pouvez tester la fonction en décommentant la fin de la fonction main_test :

$ python3 ./maze_ALAN.py -T ./graph_examples/graph1.txt  0 3 1 1 3
fonction main_test
le graphe contient 4 sommets
degré max du graphe : 3
la liste des sommets donnée forme un chemin dans le graphe

$ python3 ./maze_ALAN.py -T ./graph_examples/graph1.txt  0 3 1 1 3 2
fonction main_test
le graphe contient 4 sommets
degré max du graphe : 3
la liste des sommets donnée ne forme PAS un chemin dans le graphe

(Le fichier graph1.txt est le graphe représenté plus haut.)

N'hésitez pas à utiliser la fonction main_test pour faire d'autres tests au cours du TP.

1.2. Parcours en profondeur

Un parcours basique du graphe G à partir du sommet v0 a la forme suivante :

ATraiter = [v0]         # liste des sommets à traiter
Vu = [False] * G.N      # état des sommets
Pred = [None] * G.N     # parent des sommets dans l'arbre de parcours

while ATraiter:
    s = ATraiter.pop()

    if Vu[s]:
        continue
    Vu[s] = True

    for v in G[s]:
        if not Vu[v]:
            ATraiter.append(v)
            Pred[v] = s

Tous les sommets accessibles depuis v0 finissent dans l'arbre donné par Pred et on obtient ainsi la composante connexe du graphe contenant v0.

Codez la fonction DFS(G, v0) (pour "Depth First Search") qui fait un parcours en profondeur basique et renvoie le tableau Pred calculé.

Pour tester, il suffit de donner un argument FILENAME sur la ligne de commande, où FILENAME est un fichier contenant un graphe. La fonction DFS sera appelé sur le graph correspondant, avec une valeur de v0=0.

$ python3 ./maze_ALAN.py ./graph_examples/graph2.txt
Pred = [None, 5, 1, 2, 0, 4, 7, 3, 12, 5, 9, 15, 13, 9, 10, 14]
The corresponding tree contains 16 nodes.

Vous pouvez ignorer les mentions à v1 dans la docstring de DFS.

2. Parcours en largeur

2.1. Version naïve

Un parcours en largeur peut être obtenu à partir du parcours en profondeur basique avec 2 modifications :

on remplace le tableau ATraiter, utilisé comme un pile (avec les méthodes .append et .pop) par une file, c'est à dire une liste d'éléments où l'insertion (le "append") et la suppression (le "pop") ne se font pas du même coté ;
dans la boucle for v in G[v], on n'insère pas v dans ATraiter (ni me mets à jour Pred) si Pred[v] est déjà défini.

Écrivez la fonction BFS0 qui fait un parcours en largeur en utilisant, ATraiter.append(...) pour ajouter un élément dans ATraiter, et ATraiter.pop(0) pour retirer le premier élément (au lieu du dernier) ; et en évitant de réinsérer les voisins lorsqu'ils ont déjà un prédécesseur.

Comparez le résultat de BFS0 et DFSt sur le fichier graph2.txt. Vous pouvez préciser les fonctions de parcours avec l'option -A :

    $ python3 ./maze_ALAN.py -A DFS,BFS0 ./graph_examples/graph2.txt
    algorithm: DFS
    Pred = [None, 5, 1, 2, 0, 4, 7, 3, 12, 5, 9, 15, 13, 9, 10, 14]
    The corresponding tree contains 16 nodes.

    algorithm: BFS0
    Pred = [None, 0, 1, 2, 0, 1, 2, ..., 11]
    The corresponding tree contains 16 nodes.

Comparez l'efficacité de DFS, BFS0 sur le graphe du fichier star-100000.txt. (Il s'agit d'un graphe très simple, mais avec 100000 sommets.)
Pour voir d'où vient la différence de complexité, lancez le programme en utilisant le "profiler" de Python :
```
$ python3 -m cProfile -s tottime ./maze_ALAN.py -A BFS0 FILENAME | head -n20
...
```
Après l'exécution, Python affichera des statistiques sur le temps passé dans chaque fonction, le nombre d'appels, etc. L'argument -s tottime précise qu'il faut trier les statistiques par temps total passé dans chaque fonction. La colonne "cumtime" est également intéressante : elle contient le temps total passé dans les fonctions correspondantes, en comptant les appels aux sous-fonctions.

D'où vient la différence de complexité entre DFS et BFS0 ? ()

(Le "| head -n30" facultatif permet de n'afficher que le début du résultat, c'est à dire les fonctions qui prennent le plus de temps.)

2.2. Structure de files

Il est préférable d'utiliser une file plutôt qu'un tableau pour ATraiter. La bibliothèque standard de Python fournit une structure deque (double ended queu) où les insertions / suppressions rapides sont possibles à gauche et à droite.

$ python3
>>> from collections import deque
>>> t = deque([0,2,4,6])
>>> t
deque([0, 2, 4, 6])

>>> t.append(11)
>>> t
deque([0, 2, 4, 6, 11])

>>> t.appendleft(22)
>>> t
deque([22, 0, 2, 4, 6, 11])

>>> t.pop()
11
>>> t
deque([22, 0, 2, 4, 6])

>>> t.popleft()
22
>>> t
deque([0, 2, 4, 6])

Écrivez la fonction BFS qui fait un parcours en largeur en utilisant une structure deque.

Vous pouvez ignorer les mentions à v1 dans la docstring de BFS.
Comparez l'efficacité de BFS avec celles de BFS0 et DFS sur le graphe star-100000.txt.

2.3. Sortie anticipée : recherche de chemin

Les parcours en profondeur et en largeur partent d'un sommet et avancent dans le graphe jusqu'à avoir vu tous les sommets accessibles. Il est possible d'arrêter le parcours dès qu'un sommet particulier est rencontré. Cela permet ainsi de chercher un chemin entre deux sommets.

Modifiez vos fonctions DFS et BFS en ajoutant un argument v1 qui prend la valeur None par défaut. Votre fonction doit s'arrêter dès que le sommet s choisi dans ATraiter est égal à v1. (Dans le cas où v1 est None, le parcours continue jusqu'au bout.)
Pour retrouver le chemin entre v0 et v1 à partir du tableau Pred, il suffit de partir de v1 et de remonter dans Pred : le chemin à l'envers est simplement [v1, Pred[v1], Pred[Pred[v1]], ...]. Le chemin s'arrête lorsqu'on arrive sur v0.

Complétez la fonction pred_to_path(Pred, v0, v1) qui calcule le chemin correspondant.

Vous pourrez testez en précisant les sommets v0 et v1 avec
```
$ python3 ./maze_ALAN.py -A BFS --start 12 --end 13 ./graph_examples/graph-big1.txt
...
```
Que pensez vous du chemin trouvé par le parcours en profondeur ? Expliquez ce qui se passe.

3. Labyrinthes, avec listes d'adjacences

Un labyrinthe, du style

#################
#         #     #
# ####### # # # #
#           #   #
### ##### ##### #
#           #   #
# ####### # # # #
#   #     # #   #
# # # # ### # ###
# #   #         #
# ##### # # # # #
# #   # # # #   #
# # # # # # ### #
# #       # #   #
# # # # # # # # #
#   #   #   #   #
#################

peut être codé dans un graphe. Chaque sommet correspond à une case et les arêtes correspondent à des portes.

Cette représentation ASCII est plus visuelle que la représentation par listes d'adjacences, qui ressemble à

#%rect 8 8
1, 8
0, 9
3, 10
2, 4, 11
3, 5
4, 6
5, 7
6, 15
...
... 48 lignes
...
48, 57
49, 58, 56
57, 59, 50
58, 51
52, 61
53, 60, 62
54, 61, 63
55, 62

Attention, dans la représentation ASCII du labyrinthe, les "sommets" correspondent aux caractères ASCII à coordonnées impaires. Dans l'exemple suivant, toujours de taille 8x8, les sommets sont représentés par des ".", les portes ouvertes par des " " (espaces) et les portes fermées par des "*". Les "#" sont des "murs" et des piliers qui ne font pas vraiment partie du graphe.

#################
#. . . . .*. . .#
# #*#*#*# # # # #
#. . . . . .*. .#
#*# #*#*# #*#*# #
#. . . . . .*. .#
# #*#*#*# # # # #
#. .*. . .*.*. .#
# # # # #*# # #*#
#.*. .*. . . . .#
# #*#*# # # # # #
#.*. .*.*.*.*. .#
# # # # # # #*# #
#.*. . . .*.*. .#
# # # # # # # # #
#. .*. .*. .*. .#
#################

Les 2 exemples suivants sont des labyrinthes "5x5" : le labyrinthe où "toutes les portes sont fermées" et le labyrinthe où "toutes les portes sont ouvertes" :

###########              ###########
# # # # # #              #         #
###########              # # # # # #
# # # # # #              #         #
###########              # # # # # #
# # # # # #              #         #
###########              # # # # # #
# # # # # #              #         #
###########              # # # # # #
# # # # # #              #         #
###########              ###########

3.1. Résolution

Une technique connue pour sortir d'un labyrinthe est la méthode de la main droite : on met sa main sur le mur de droite et on avance en gardant toujours le contact avec le mur.

Est-ce que cette méthode permet toujours de sortir d'un labyrinthe ? Autrement dit, est-on sûr de parcourir tout le labyrinthe et donc de passer un jour sur la case "sortie" ?
Cette méthode s'apparente t'elle plutôt à un parcours en largeur ou un parcours en profondeur ? L'autre parcours est il applicable facilement pour sortir d'un vrai labyrinthe ?
Comment peut-on améliorer la méthode de la main droite pour garantir qu'on va trouver la sortie ?

Vous pouvez visualiser le chemin trouvé avec une commande de la forme python3 ./maze_ALAN -A BFS --start=X,Y --end=X,Y FILENAME où

BFS peut être remplacé par un autre algorithme
X et Y sont les coordonnées des cases de départ et d'arrivée
W et H sont la largeur et hauteur du labyrinthe
FILENAME est un fichier contenant le graphe d'une grille.

Par exemple :

$ python3 ./maze_ALAN.py -A DFS --start=0,0 --end=0,7 maze_examples/maze-8x8.txt
found a path of length 34
#################
#@ . . . .#. . .#
# ####### # # # #
#x     x . .#x .#
### ##### ##### #
#      x . .#. .#
# ####### # # # #
#   #x . .#.#. x#
# # # # ### # ###
# #   #. . . . x#
# ##### # # # # #
# #. .#x#.#x#x x#
# # # # # # ### #
# #. . . .#x#x x#
# # # # # # # # #
#$ .#. .#x x#x x#
#################

Les symboles utilisés sont les suivants :

"@" et "$" pour les points de départ et d'arrivée choisis (--start et --end),
"." pour les cases du chemin trouvé,
"x" pour les cases explorées mais qui ne font pas partie du chemin trouvé,
" " (espace) pour les cases non explorées par l'algorithme.

Pour mieux visualiser le chemin, vous pouvez utiliser grep pour mettre les . en couleur :

$ python3 ./maze_ALAN.py -A DFS --start=0,0 --end=0,7 maze_examples/maze-8x8.txt  |  grep --color '[@$.]\?'
found a path of length 34
#################
#@ . . . .#. . .#
# ####### # # # #
#x     x . .#x .#
### ##### ##### #
#      x . .#. .#
# ####### # # # #
#   #x . .#.#. x#
# # # # ### # ###
# #   #. . . . x#
# ##### # # # # #
# #. .#x#.#x#x x#
# # # # # # ### #
# #. . . .#x#x x#
# # # # # # # # #
#$ .#. .#x x#x x#
#################

Comparez les chemins trouvés par le parcours en largeur et profondeur dans les labyrinthes du répertoire maze_examples.

Comment expliquez vous les différences trouvées ?

Vous pouvez supprimer l'affichage du labyrinthe avec l'option --quiet / -q. C'est pratique pour les gros labyrinthes.

3.2. Génération

Un parcours extrait un arbre couvrant (donné par le tableau Pred) d'un graphe. Toutes les arêtes de cet arbre sont des arêtes du graphe de départ. Si on fait un parcours sur une grille où toutes les portes sont ouvertes, cela revient à choisir des portes que l'on souhaite verrouiller. Le résultat est donc un labyrinthe particulier.

Pour tester, vous pouvez utiliser la commande suivante, sans préciser de nom de fichier :

$ python3 ./maze_ALAN.py -A DFS --rect=4x4 --start=2,2                                                                                                              [22:05] +23
#########
#   #   #
# ### # #
# #   # #
# # ### #
# # # # #
# # # # #
#   #   #
#########

L'argument --rect=4x4 précise qu'on veut partir d'une grille rectangulaire de taille 4x4, et l'argument --start donne le point de départ v0 du parcours. (L'argument --end est ignoré dans ce cas.)

Que pensez vous des labyrinthes générés par le parcours en largeur et le parcours en profondeur ? Testez sur des labyrinthes plus grands que 4x4, comme 40x10, avec un point de départ au centre du labyrinthe (--start=20,5).
Écrivez la fonction random_search(G, v0, v1=None) qui fait un parcours aléatoire du graphe : à chaque étape de la boucle, on choisit au hasard un élément de ATraiter.

Faites attention à la complexité de votre fonction, qui devra éviter des calculs superflus.
Les labyrinthes générés (en utilisant -A random_search) sont ils satisfaisants ?

L'option --randomize permet de "mélanger" le graphe avant de lui appliquer l'algorithme choisit. La structure du graphe ne change pas, mais l'ordre des voisins est modifiée aléatoirement.

$ python3 ./maze_ALAN.py -A BFS --rect=4x4 --start=2,2 --randomize
...

Que pensez vous des labyrinthes générés par le parcours en largeurs et en profondeur sur des grilles mélangées de cette façon ?

3.3. Challenge : création d'un labyrinthe intéressant (facultatif)

En gravant un labyrinthe sur le tour d'un cylindre, on peut créer une "boite casse-tête" où, pour ouvrir la boite, il faut résoudre un labyrinthe.

L'objectif de cette partie (facultative) est de proposer un labyrinthe intéressant à imprimer en 3D pour fabriquer une telle boite.

Proposez un labyrinthe intéressant sur une grille 16x10 et expliquez pourquoi il est particulièrement intéressant.

Des consignes et pistes de réflexion sont données plus bas.

Consignes

Le labyrinthe gagnant sera imprimé en 3D sur un cylindre. Autrement dit, on peut mettre des passages entre la partie droite et la partie gauche du labyrinthe. Ces labyrinthes "cylindriques" peuvent être générés avec l'option --cyl :

$ python3 ./maze_ALAN.py -r --cyl 8x5
################
          #   #   > passage vers la gauche
# ### ### # # ##
#   # #   # #
##### # ### ###
      # # #   #   > passage vers la gauche
####### # ### ##
#   #   # #   #
# # # ### # ###
  #       # #     > passage vers la gauche
################

Votre labyrinthe devra avoir une taille de 16x10, soit 32 caractères de large et 21 caractères de haut.

Il devra également avoir une entrée sur la dernière ligne et une sortie sur la première ligne :

##################### ##########
            #   #   # #       #
########### # # # # # # ##### #
          # # #   #   # #     #
######### # # ####### # # #####
    #   # # # # #   # # #   #
##### # # # # # # # # ##### # ##
  #   #   # # # # # # #   # # #
# # ####### # # # # # # # # ###
# # #     #   #   #   # # #
# # # ### ##### ####### # ######
#   #   #   # # #     # #   #
######### # # # # ### ### ### #
      #   # # #   # #   #     #
##### # ### # ##### ### # #####
#   #   # #         #   # #
# # ##### ######### # ### # ####
  # #           #   #   # #   #
### # ### ####### ##### ##### #
  #     #             #       #
######### ######################

Pistes de réflexion

Il y a plusieurs manières de rendre vos labyrinthes plus intéressants. Voici quelques idées.

Vous pouvez supprimer les culs de sacs en écrivant la fonction braid_maze(G, M). La fonction sera appelée si vous ajouter l'option -B 1 / --braid=1 à la commande.

Cela vous permettra d'obtenir des labyrinthes du style
```
$ python3 ./maze_ALAN.py -rB --cyl 8x5
################
      #       #
# # # # ### # #
# #   #     #
# ### ##########
    #   #
# # ### # ######
# # #   # #
# # # ### # ###
#
################
```
Vous pouvez choisir l'entrée et la sortie pour essayer de rendre le labyrinthe plus facile ou plus difficile.

Vous pouvez "enlever" une partie de la grille. Par exemple, si vous utilisez la grille suivante

    ################################

    # # # # # # # # # # # # # # # #

    # # # # # # # # # # # # # # # #

    # # # ################# # # # #
          #               #
    # # # # # # # # # # # # # # # #
          #               #
    # # # # # # # # # # # # # # # #
          #               #
    # # # # # # # # # # # # # # # #
          #               #
    # # # ################# # # # #

    # # # # # # # # # # # # # # # #

    # # # # # # # # # # # # # # # #

    ################################

le labyrinthe aura une partie centrale inaccessible. Vous pourrez y ajouter quelque chose dans cette partie une fois le labyrinthe généré. (exemple et le rendu 3D)

Voici le code utilisé dans la fonction main_test pour cet exemple :

G = CylinderGrid.from_grid("grille.txt")
Pred = random_search(G, 0)
M = CylinderGrid.pred2graph(Pred, G.width, G.height)    # transformer le tableau Pred en graphe
braid_maze(G, M)                                        # suppression des culs de sac
M.show()

Vous pouvez même créer votre labyrinthe entièrement à la main si vous le souhaitez.

4. "Labyrinthes", sans listes d'adjacences

4.1. Préliminaire

Le problème suivant est adapté d'un problème tiré d'un concours de programmation.

L'objectif est de trouver le plus court chemin (en nombre d'étapes) pour sortir d'une pièce contenant des obstacles. L'entrée du problème est de la forme (obstacle-fixed.txt)

#@####################
#.x........x.x.xx....#
#.....x.x.xx......xx.#
#......xx.xxxx.xx....#
#x.x....x......xx...x#
#x.x...xxxx....x.....#
#x.xxxxxxxx......xxx.#
#x......x..xxxx.xx.x.#
#x.xxxx.x..xx......x.#
#...x...xx.xx.xxxxxx.#
#x.x...x.............#
#x...xx..xxxxx.xx.xx.#
#x..xx..xxx.....xx...#
#..x...xxxx.xxx....x.#
####################$#

- La case @ (toujours en haut à gauche) est le point de départ et la case $ (toujours en bas à droite) est le point d'arrivée.

Les case # sont des murs.
Les cases . sont des cases libres, sur lesquelles on peut se déplacer.
Il n'est pas possible de se déplacer en diagonale.

Attention, par rapport aux labyrinthes de la partie précédente où seuls les caractères de coordonnées impaires étaient des sommets du graphe, tous les caractères (sauf les #) sont des sommets du graphe.

Complétez la définition de la fonction find_path_fixed du fichier obstacles_ALAN.py qui fait un parcours en largeur pour trouver un chemin de la case @ à la case $.

La fonction prend un argument M : c'est un tableau à 2 dimension donnant l'état initial du labyrinthe sans les murs externes #. Par exemple, pour le labyrinthe

#@####
#..x.#
#..xx#
#x...#
#....#
####$#

le tableau M contient

[
  ['.', '.', 'x', '.'],
  ['.', '.', 'x', 'x'],
  ['x', '.', '.', '.'],
  ['.', '.', '.', '.']
]

La fonction doit renvoyer un tableau C contenant les positions successives qui amènent à la sortie. La première case C est donc toujours (0, -1), et sa dernière case est toujours (WIDTH-1, HEIGHT).

S'il n'y a pas de solution, la fonction devra renvoyer [].

Attention, pour accéder à la case de coordonnées (x,y), il faut faire M[y][x].
L'entrée, de coordonnées (0, -1) et la sortie, de coordonnées (WIDTH-1, HEIGHT) ne font pas partie du tableau et devront être traitées comme des cas particuliers.
Vous ne devez pas transformer le tableau M en un graphe (listes d'adjacences par exemple) mais devez utiliser directement le tableau M pour retrouver les voisins de chaque case au fur et à mesure.
Comme les sommets ne sont pas des entiers, mais des coordonnées de cases, il est pratique de remplacer les tableaux Vu et Pred par
- un ensemble de sommets pour Vu (Vu = set(), avec la méthode Vu.add(s) pour ajouter un élément),
- un dictionnaire Pred, utilisé exactement comme un tableau.
La file ATraiter sera toujours une file (deque), qui contiendra des paires.

Vous pouvez tester avec

$ python3 ./obstacles-ALAN.py --fixed FICHIER

$ python3 ./obstacles-ALAN.py --fixed --show-solution FICHIER

si vous voulez afficher toutes les étapes de la solution.

Comme pour les premières parties, vous pouvez appeler la fonction main_test avec l'argument -T.
```
$ python3 ./obstacles-ALAN.py -T ...
```
Lisez la documentation de cette fonction pour comprendre comment elle fonctionne, et n'hésitez pas à la modifier pour faire vos propres tests !

Analysez et comparer les tailles de la représentation d'un labyrinthe :

comme tableau M comme dans la question précédente,
et comme tableau de listes d'adjacences comme dans les parties précédentes.

Vous devez pour ceci imaginer comment vous transformeriez le tableau M en tableau Voisin, et quelle serait la taille des données correspondantes.

Quelles structure de données vous parait la plus appropriée pour ce problème ?

4.2. Version générale : obstacles mobiles

Description du problème

Le "labyrinthe" peut maintenant contenir des obstacles mobiles. L'entrée du problème est de la forme (obstacle4.txt)

#@################
#^.>v..>>.^.>..<.#
#..<>..<>v.^.vvv.#
#..v.v.v<..^.<.^.#
#^..>..>.v..<>.v.#
#..<..<.v.>..>.^.#
#.>.>..>v..v<..>.#
################$#

La case @ (toujours en haut à gauche) est le point de départ et la case $ (toujours en bas à droite) est le point d'arrivée.
Les case # sont des murs.
Les cases . sont des cases libres, sur lesquelles on peut se déplacer.
Les cases >, <, v, ^ et x sont des obstacles.
Il n'est pas possible de se déplacer en diagonale, mais il est possible de rester sur place.

Les obstacles sont mobiles. À chaque étape :

> se déplace vers la droite,
< se déplace vers la gauche,
^ se déplace vers le haut,
v se déplace vers le bas,
x est fixe et ne se déplace pas.

Lorsqu'un obstacle atteint un mur #, il réapparait en face :

  t = 1    t = 2    t = 3    t = 4    t = 5
  #E####   #E####   #E####   #E####   #E####
  #.>..#   #..>.#   #...>#   #>...#   #.>..#    etc.
  #....#   #....#   #....#   #....#   #....#
  ####$#   ####$#   ####$#   ####$#   ####$#

L'objectif de cette partie est de chercher un trajet le plus court possible (en nombre d'étapes) pour aller de l'entrée à la sortie en évitant tous les obstacles.

Initialement, les cases ne contiennent qu'un seul obstacle, mais elles peuvent par la suite en contenir plusieurs. Ils n'interagissent pas entre eux

  t = 1    t = 2    t = 3    t = 4    t = 5
  #E####   #E####   #E####   #E####   #E####
  #.>..#   #..>.#   #...*#   #>...#   #.>..#    etc.
  #...x#   #...*#   #...x#   #...x#   #...*#
  #...^#   #....#   #....#   #...^#   #....#
  ####$#   ####$#   ####$#   ####$#   ####$#

Au temps t=2, la case * contient 2 obstacles : un ^ et un x ; et à t=3, la case * contient 2 obstacles : un > et un ^.

Exemples

Pour le labyrinthe (obstacles_examples/obstacle1.txt)

#@#####
#<>...#
#v..<v#
#<..^.#
#####$#

on peut atteindre la sortie à l'étape 9 (obstacles_examples/obstacle1.sol) :

t = 0       t = 1       t = 2
#@#####     # #####     # #####
#<>...#     #@.>.<#     #v@.*v#
#v..<v#     #..<^.#     #.<...#
#<..^.#     #v...*#     #...<.#
#####$#     #####$#     #####$#
 
 
t = 3       t = 4       t = 5
# #####     # #####     # #####
#.@<.>#     #><@..#     #*>.^v#
#*...v#     #...^<#     #..@<.#
#..<^.#     #v<..v#     #<....#
#####$#     #####$#     #####$#
 
 
t = 6       t = 7       t = 8
# #####     # #####     # #####
#..>.<#     #...*.#     #v.<^*#
#v.<@v#     #.<.^@#     #<....#
#...^<#     #v..<v#     #..<.@#
#####$#     #####$#     #####$#
 
 
            t = 9
            # #####
            #><...#
            #v...*#
            #.<.^.#
            #####@#

Notez que le personnage @ reste au même endroit entre t=2 et t=3, c'est un déplacement autorisé.

Les déplacements du personnage et des obstacles sont instantanés et seuls leurs positions aux temps "entiers" est importante. Par exemple, le déplacement entre t=3 et t=4 est possible car la case occupé par @ à t=4 est libre. Le fait que le personnage se déplace vers la droite et "traverse" en obstacle qui se déplace vers la gauche n'est pas important.

Le labyrinthe (obstacles_examples/obstacle2.txt)
```
#@#####
#<>vx^#
#vv<<x#
#<x>^v#
#####$#
```
a une solution en 15 étapes (obstacles_examples/obstacle2.sol).
Le labyrinthe (obstacles_examples/obstacle3.txt)
```
#@###
#><.#
#<>.#
#...#
###$#
```
n'a pas de solution.

Parcours en largeur "paresseux"

Dans ce problème, le graphe des déplacement a pour sommets les cases du labyrinthe aux temps t=0, t=1, ... ; et les arêtes correspondent aux déplacements possibles : x0,y0,t --> x1,y1,t+1.

Pour éviter de construire ce graphe en entier, nous allons écrire un parcours en largeur (comme pour la question précédente) paresseux, càd en construisant le graphe au fur et à mesure des besoins.

Lors d'un parcours en largeur du graphe, on commence par la case @ au temps 0, puis on regarde ses voisins au temps 1, puis leurs voisins au temps 2, etc. On ne revient jamais en arrière et il n'est donc pas nécessaire de garder le tableaux des cases à tous les temps possibles.

Le parcours ressemblera donc à celui de la question précédente, mais :

Les cases sont identifiées par leurs coordonnées et le temps correspondant.
Les cases voisine d'une cases sont les voisines au temps suivant qui ne contiennent pas d'obstacle.
On conserve une variable temps_courant dans la fonction, avec l'état du labyrinthe à temps_courant+1 pour tester les cases voisines.
Lorsqu'on récupère une case dans la file ATraiter :
- soit c'est une case au temps temps_courant, auquel cas on continue l'algorithme normalement,
- soit c'est une case au temps temps_courant+1, auquel cas il faut mettre le labyrinthe à jour en déplaçant les obstacles mobiles et incrémentant temps_courant. Une fois que c'est fait, on continue l'algorithme normalement.
Les autres possibilités n'arrivent jamais sauf en cas de bug de votre part. (Je vous conseille de mettre un assert dans votre code afin de détecter un bug à ce niveau là !)j

Écrivez le corps de la fonction find_path dans le fichier obstacles_ALAN.py.

La fonction prend un argument M : c'est un tableau à 2 dimension donnant l'état initial du labyrinthe. Par exemple, pour le labyrinthe (obstacles_examples/obstacle1.txt)
```
#E#####
#<>...#
#v..<v#
#<..^.#
#####$#
```
le tableau M contient
```
[
  ['<', '>', '.', '.', '.'],
  ['v', '.', '.', '<', 'v'],
  ['<', '.', '.', '^', '.']
]
```
Vous devez renvoyer un tableau C contenant les positions successives qui amènent à la sortie. La première case C est donc toujours (0, -1), et sa dernière case est toujours (WIDTH-1, HEIGHT).
Le répertoire obstacles_examples/ contient plusieurs exemples :
- obstacle1.txt (avec une solution dans obstacle1.sol)
- obstacle2.txt (avec une solution dans obstacle2.sol)
- obstacle4.txt (solution possible en 27 étapes)
- obstacle5.txt (solution possible en 246 étapes)
- obstacle6.txt (solution possible)
- obstacle7.txt (solution possible, si votre programme est un peu optimisé)

Vous pouvez supposer que tous les labyrinthes ont une solution.
Faites attention à ne pas "perdre" d'obstacle lorsque plusieurs d'entre eux se retrouvent sur la même case. Le plus simple est de conserver une liste avec tous les obstacles et leurs positions, que vous pourrez mettre à lorsque c'est nécessaire.

Écrivez le corps de la fonction show_path pour pouvoir visualiser vos solutions avec

$ python3 obstacles_ALAN.py --show-solution FICHIER

Ajoutez la gestion des labyrinthes sans solution. La fonction find_path devra dans ce cas renvoyer [].

Documentez ce que vous faites.

INFO601 : algorithmes et graphes

TP 1 : parcours de graphes, labyrinthes

Printemps 2024

Consignes

Liens utiles

1. Préliminaires : listes d'adjacences

1.1. Représentation des graphes

1.2. Parcours en profondeur

2. Parcours en largeur

2.1. Version naïve

2.2. Structure de files

2.3. Sortie anticipée : recherche de chemin

3. Labyrinthes, avec listes d'adjacences

3.1. Résolution

3.2. Génération

3.3. Challenge : création d'un labyrinthe intéressant (facultatif)

Consignes

Pistes de réflexion

4. "Labyrinthes", sans listes d'adjacences

4.1. Préliminaire

4.2. Version générale : obstacles mobiles

Description du problème

Exemples

Parcours en largeur "paresseux"