Consignes
Le rendu de ce TP se fera uniquement par TPLab et consistera en une archive (zip, tar, etc.) contenant un répertoire TP2-NOM avec :
-
votre fichier NOM-deduction_naturelle.v
-
votre fichier NOM-concat.v
-
un fichier texte README contenant les réponses aux questions du TP
-
tout autre fichier que vous jugerez pertinent (fichiers de tests, graphiques, benchmarks, etc.)
-
Vous aurez compris que NOM devra être remplacé par votre nom (ou vos noms en cas de binômes) !
Tous vos fichiers doivent comporter une entête avec votre noms et votre groupe de TP.
Tout non respect d'une ou plusieurs de ces consignes entrainera automatiquement un retrait de points sur votre note !
Outils nécessaires, prérequis
Pour ce TP, vous devez disposer de l'assistant de preuves Coq. Sur les machines de l'université, Coq est installé sur la partition Linux.
Nous allons utiliser l'éditeur de texte emacs avec l'extension Proof General.
Si vous utilisez votre portable, vous devez arriver en TP avec un système fonctionnel. Pour Ubuntu, lancez la commande
$ sudo apt install coq emacsTout le TP a également été testé sur l'interface en ligne https://coq.vercel.app/scratchpad.html, mais cela nécessitera de copier/coller dans un fichier texte externe pour sauvegarder votre travail.
Installation de Proof General (sauf pour l'interface en ligne)
Lancez la commande suivante depuis un terminal, pour télécharger, compiler et configurer Proof General automatiquement. Ça devrait prendre moins de une minute. (Attention, il faut copier toutes les lignes de la commande, sans le $ initial.)
$ [ -d ~/.emacs.d/lisp/PG ] ||
git clone https://github.com/ProofGeneral/PG ~/.emacs.d/lisp/PG &&
make -C ~/.emacs.d/lisp/PG &&
grep -qs 'Proof General config' ~/.emacs ||
{ echo '; Proof General config' >> ~/.emacs &&
echo '(load "~/.emacs.d/lisp/PG/generic/proof-site")' >> ~/.emacs &&
echo '(setq inhibit-startup-screen t)' >> ~/.emacs &&
echo '(setq proof-splash-enable nil)' >> ~/.emacs &&
echo '(setq coq-accept-proof-using-suggestion (quote never))' >> ~/.emacs ; }Liens utiles
-
le fichier exemple_surjection.v
-
le fichier mario_deduction_naturelle.v
-
le fichier mario_concat.v
-
Software Foundations, une série très complète sur l'application des assistants de preuves à l'analyse de programmes.
Préliminaires
Utiliser Coq
Coq est un assistant de preuves développé par l'INRIA. Contrairement aux SAT-solveurs (par exemple), les preuves dans un tel système ne sont en général pas automatiques : les assistants de preuves nécessitent une interaction avec l'utilisateur. Cela permet de faire de preuves plus complexes qu'on ne peut pas automatiser.
Coq est basé sur le calcul des constructions, qui peut être vu comme une extension de la déduction naturelle et des langages de programmation fonctionnelle. (Coq est d'ailleurs programmé en Caml.)
Une preuve en Coq se déroule de la manière suivante.
-
On définit (mot clé
Definition) les types pour les objets que l'on veut manipuler. Coq possède de nombreuses bibliothèques avec les types des objets usuels : nombres, listes, etc. -
On donne un énoncé que l'on veut prouver (mot clé
Theorem) en donnant la proposition ("formule") correspondante. -
On fait la preuve en utilisant des "tactiques" de preuves. Ces tactiques généralisent les "règles de démonstrations" vues en cours. L'interpréteur Coq vérifie que chaque étape est valide et affiche le but courant.
-
On termine la preuve avec le mot clé
Qed(abbréviation de "Quod erat demonstrandum", càd "Ce qu'il fallait démontrer" en latin).
Un exemple
Le fichier exemple_surjection.v contient une petite preuve en Coq. Pour comprendre comment une preuve Coq fonctionne, ouvrez ce fichier dans emacs. Si vous avez bien installé Proof General, vous devriez obtenir
Les preuves en Coq ne sont en général pas lisibles "statiquement". Avancez dans la preuve en utilisant le bouton "Next" (triangle vert vers le bas dans l'interface en ligne) pour observer ce qu'il se passe :
-
définition de
surjectiveetcomp, -
énoncé du théorème,
-
preuve.
Lors de la preuve, Coq affiche le but courant ("goal" en anglais). Le but ressemble à un séquent, mais les hypothèses sont notées au dessus de la formule plutôt qu'à gauche. Par exemple, à cette étape de la preuve,
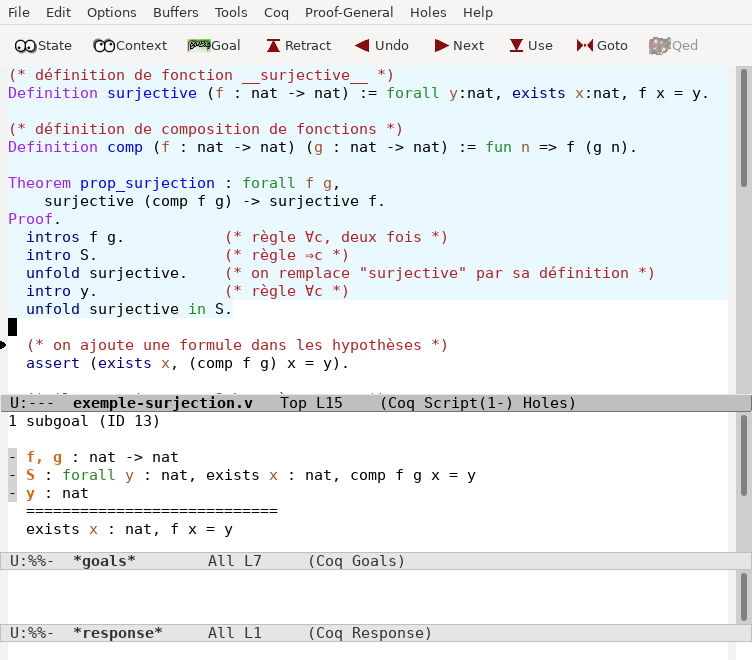
les hypothèses contiennent
-
la liste des variables avec leurs types :
-
f et g de type ℕ → ℕ (première ligne)
-
y de type ℕ (troisième ligne),
-
-
la formule ∀y:ℕ, ∃x:ℕ, f∘g(x) = y (deuxième ligne).
Comme les variables ne sont pas déclarées explicitement dans les séquents, ceci correspond au séquent
| ∀y:ℕ, ∃x:ℕ, f∘g(x) = y ⊢ ∃x:ℕ, f(x) = y |
Avancez dans la preuve en regardant l'évolution du but.
-
Donnez le but (sous forme de séquent) à la ligne "(* QUEL EST LE BUT COURANT ICI *)"
-
Que se passe t'il quand vous essayez de finir la preuve (commande
Qed) ? -
ajoutez la tactique
assumption.(qui correspond à la règle "axiome") juste avant la commandeQedet vérifiez que cela permet de finir la preuve.
Emacs et Proof General offrent les raccourcis suivants :
-
"Next" (pour avancer d'une étape dans la preuve) : "Control-c-n",
-
"Undo" (pour reculer d'une étape dans la preuve) : "Control-c-u",
-
"Goto" (pour aller jusqu'au curseur dans la preuve) : "Control-c-Enter",
-
"Use" (pour aller à la fin du fichier en vérifiant les preuves) : "Control-c-b".
1. Déduction naturelle en Coq
1.1. Règles et tactiques
En utilisant les même noms utilisés en cours et en TD (voir regles.pdf), les règles de la déduction naturelle correspondent aux tactiques suivantes.
| règle | tactique | remarques | |
|---|---|---|---|
| axiome | *+ |
assumption.
|
|
| ⇒c | * |
intro.
|
on peut choisir le nom de l'hypothèse avec intro H.
|
| ⇒h / modus ponens |
apply H.
|
H doit être une hypothèse ou un théorème de la forme P -> Q
|
|
| ∧c | * |
split.
|
|
| ∧h | + |
destruct H.
|
H doit être une hypothèse ou un théorème de la forme F /\ G
|
| ∨c,1 |
left.
|
||
| ∨c,2 |
right.
|
||
| ∨h / raisonnement par cas | + |
destruct H.
|
H doit être une hypothèse ou un théorème de la forme F \/ G
|
| ¬c | * |
intro.
|
on peut choisir le nom de l'hypothèse avec intro H.
|
| ¬h / contradiction |
apply H.
|
H doit être une hypothèse ou un théorème de la forme ~P
|
|
| ∀c | * |
intro.
|
on peut choisir le nom de la variable avec intro x.
|
| ∀h / spécialisation |
apply H.
|
H doit être une hypothèse ou un théorème de la forme forall x, F
|
|
| ∃c |
exists (u).
|
u est le terme qui sert de témoin
|
|
| ∃h / utilisation du ∃ | + |
destruct H.
|
H doit être une hypothèse ou un théorème de la forme exists x, F
|
| résultat intermédiaire |
assert H.
|
H est la formule que l'on veut ajouter aux hypothèses
|
|
| raisonnement par l'absurde |
apply NNPP; intro.
|
il faut avoir la ligne Require Import Classical_Prop. au début du fichier
|
-
Vous pouvez toujours appliquer une tactique "*",
-
vous pouvez toujours appliquer une tactique "+" sur une hypothèse.
Une première preuve
Dans votre fichier mario_deduction_naturelle.v complétez les preuves suivantes :
Theorem et_1 : P /\ Q -> P.
Proof.
(* ... *)
(tactiques assumption., destruct. et
intro.)
et
Theorem et_2 : P /\ Q -> Q.
Proof.
(* ... *)
(tactiques assumption., destruct. et
intro.)
1.2. Déduction naturelle, logique propositionnelle
Il est possible de faire une preuve en donnant simplement les tactiques dans l'ordre. L'interpréteur retrouve automatiquement le but courant à chaque étape, et passe au but suivant lorsqu'un but est prouvé.
Il est cependant conseillé d'utiliser les marqueurs de liste ("-", "+" et "*") pour séparer les preuves des différents buts. Ainsi, une preuve pourrait ressembler à
Theorem ...
Proof.
tactique1.
tactique2.
tactique3.
- tactique4.
tactique5.
+ tactique6.
+ tactique7.
tactique8.
- tactique9.
tactique10.
Dans cette preuve,
-
les tactique 1 à 3 s'appliquent au but initial,
-
la tactique 3 introduit un nouveau sous-but,
-
le premier sous-but est prouvé par les tactiques 4 à 8,
-
la tactique 5 introduit un nouveau sous-but,
-
le premier "sous-sous-but" est prouvé par la tactique 6,
-
le second "sous-sous-but" est prouvé par les tactiques 7 et 8,
-
-
le second sous-but est prouvé par les tactiques 9 et 10.
Faites les preuves suivantes en Coq dans votre fichier mario_deduction_naturelle.v.
Theorem et_com : P /\ Q -> Q /\ P.
(tactiques destruct, split, et intro)
Theorem ou_com : P \/ Q <-> Q \/ P.
(tactiques destruct, left, right,
split et intro)
Theorem contraposition : (P -> Q) -> (~Q -> ~P).
(tactique apply et intro)
Theorem distribution : (P \/ (Q /\ R) -> (P \/ Q) /\ (P \/ R)).
(tactiques destruct, left, right,
split et intro)
Plus difficile, faites la preuve de la première loi de de Morgan :
| ¬(P ∨ Q) ⇔ ¬P ∧ ¬Q |
(tactiques apply, destruct, left,
right, split et intro)
Faites la preuve de la deuxième loi de de Morgan :
| P ∨ Q ⇔ ¬(¬P ∧ ¬Q) |
En plus des tactiques apply, destruct,
left, right, split et
intro, vous aurez besoin du raisonnement par l'absurde :
apply NNPP; intro.
1.3. Déduction naturelle, logique du premier ordre
On ajoute maintenant les quantificateurs !
Faites les preuves suivantes en Coq.
Theorem pourtout_et : (forall x:X, (P x /\ Q x)) <-> (forall x : X, P x) /\ (forall x : X, Q x).
(tactiques apply, destruct, split et
intro)
Theorem existe_ou : (exists x:X, (P x \/ Q x)) <-> (exists x:X, P x) \/ (exists x:X, Q x).
(tactiques destruct, exists, left,
right, split et intro)
Plus dur, faite la preuve de la loi de de Morgan
| ¬∃ x:X, P(x) ⇔ ∀ x:X, ¬ P(x) |
(tactiques apply, destruct, exists,
split et intro)
La tactique apply prend comme argument une hypothèse ou un
théorème déjà démontré.
Si l'hypothèse ou le théorème est de la forme ∀ x, ..., on peut
utiliser apply (H u). pour utiliser une instanciation
particulière.
Faites la preuve de la loi de de Morgan
| ∃ x:X, P(x) ⇔ ¬(∀ x:X, ¬P(x)) |
En plus des tactiques apply, destruct,
exists, split et intro, vous aurez
besoin du raisonnement par l'absurde : apply NNPP; intro.
2. Initiation à la preuve de programmes
Les assistants de preuves sont également utilisés pour faire des preuves de programmes. L'objectif est de vérifier qu'un programme satisfait sa spécification. On pourrait par exemple montrer
Theorem tri_insertion_correct :
forall l : list nat,
dans_l_ordre (tri_insertion l) /\ est_permutation l (tri_insertion l)
Il faudrait bien sûr commencer par :
-
définir le programme
tri_insertion, -
définir le prédicat
dans_l_ordre, -
définir le prédicat
est_permutation.
La preuve complète nécessiterait l'introduction de nombreux concepts. Nous allons donc nous intéresser à des programmes moins complexes.
2.1. Concaténation des listes
Même s'il est possible de prouver des programmes écrits en C ou en Java, il est nettement plus simple de regarder des programmes écrits dans un langage fonctionnel.
Le type des listes chainées est déjà défini en Coq. Il suffit simplement d'importer la bonne bibliothèque :
Require Import List.
Import ListNotations.
Comme en Caml, le type des listes est un type récursif avec 2 constructeurs :
-
[]désigne la liste vide, -
e::ldésigne l'ajout du l'élémentedevant la listel.
La concaténation s'écrit presque comme en Caml :
Fixpoint concat (l1 : list nat) (l2 : list nat) :=
match l1 with
| [] => l2
| x::l1 => x :: (concat l1 l2)
end.
Rappel, la concaténation en Caml peut s'écrire comme
let rec concat l1 l2 =
match l1 with
| [] -> l2
| x::l1 -> x::(concat l1 l2)
Vous pouvez faire quelques tests dans emacs en évaluant les commandes suivantes :
Compute (concat [] []).
Compute (concat [1; 2; 3] []).
Compute (concat [] [65; 66; 67]).
Compute (concat [1; 2] [65; 66; 67; 68]).
qui donneront respectivement [], [1;2;3],
[65; 66; 67] et [1; 2; 65; 66; 67; 68].
Par définition, pour n'importe quelle liste l, on devrait avoir
concat [] l = l. Dans votre fichier mario_concat.v,
faites la preuve de
Theorem concat_vide_gauche : forall l : list nat, concat [] l = l.
Vous devrez utiliser la tactique simpl. pour simplifier
(évaluer) une hypothèse ou un but.
Pour prouver un but évident, vous pouvez utiliser la tactique
trivial.
Essayez de faire la même preuve pour
Theorem concat_vide_droite : forall l : list nat, concat l [] = l.
et expliquez brièvement dans un commentaire pourquoi cela ne fonctionne pas.
Ne cherchez pas de preuve correcte pour cette formule. Cela sera fait dans la question suivante !
2.2. Preuves par induction
La preuve de
Theorem concat_vide_droite : forall l : list nat, concat l [] = l.
nécessite une nouvelle tactique pour faire des preuves par récurrence :
-
si une propriété est vraie pour
[], -
et si quand cette propriété est vraie pour
l, alors elle est vraie pourx::l,
alors la propriété est vraie pour n'importe quelle liste.
En effet,
-
la propriété est vraie pour
[]par le point 1, -
comme la propriété est vraie pour
[], elle est vraie pourx::[] = [x]par le point 2, -
comme la propriété est vraie pour
[x], elle est vrai poury::[x] = [x; y]par le point 2, -
...
Si l est une variable de liste dans le contexte, la tactique
induction l. va générer 2 buts :
-
un sous-but pour
[], -
un sous-but pour
x::l, en ajoutant l'hypothèse que le but courant est vrai pourl.
Faite la preuve par induction du résultat suivant.
Theorem concat_vide_droite : forall l : list nat, concat l [] = l.
-
vous devrez utiliser la tactique
inductionsur la listelaprès avoir fait unintro., -
vous pouvez utiliser la tactique
simpl.pour simplifier le but courant, -
vous pouvez utiliser la tactique
trivial.pour finir une preuve vraiment facile, -
si vous avez une hypothèse
H : u = v, vous pouvez remplacer chaqueuparvdans le but courant avec la tactiquerewrite H.
Faite la preuve par induction que la concaténation est associative :
Theorem concat_associative : forall l1 l2 l3,
concat (concat l1 l2) l3 = concat l1 (concat l2 l3).
Les tactiques utilisées seront les même que pour la question précédente.
Une seule induction (sur l1) est suffisante pour faire cette
preuve.
2.3. Deux manières de renverser une liste
La manière "naïve" de renverser une liste consiste à prendre la tête de liste et à la concaténer à la fin du renversé de la queue de liste. En Coq :
Fixpoint renverse (l : list nat) :=
match l with
| [] => []
| x::l => concat (renverse l) [x]
end.
Une autre manière, plus efficace, est d'utiliser la fonction suivante avec un accumulateur :
Fixpoint concat_renverse (l1 : list nat) (l2 : list nat) :=
match l1 with
| [] => l2
| x::l1 => concat_renverse l1 (x::l2)
end.
On obtient alors le renversé de l avec concat_renverse l
[].
En Caml, les fonctions correspondantes pourraient s'écrire de la manière suivante.
let rec renverse l =
match l with
| [] -> []
| x::l -> (concat (renverse l) [x])
let rec concat_renverse l1 l2 =
match l1 with
| [] -> l2
| x::l1 -> concat_renverse l1 (x::l2)
Essayez de faire une preuve par induction de
Theorem thm_renverse : forall l, renverse l = concat_renverse l [].
et expliquez en quelques mots pourquoi ce n'est pas possible directement.
Avant de prouver le théorème de la question précédente, nous allons prouver un théorème plus général :
Theorem thm_renverse_gen : forall l1 l2,
renverse_concat l1 l2 = concat (renverse l1) l2.
Faite cette preuve par induction sur l1 en faisant attention aux
points suivants :
-
utilisez la tactique
induction l1.avant de d'ajouterl2dans le contexte courant, -
il n'est pas nécessaire de faire une induction sur
l2, -
vous aurez une hypothèse d'induction de la forme
IHl1 : forall l2, ... = .... Vous pouvez utilisez(IHl1 l3)pour spécialiser cette hypothèse à n'importe quelle listel3. -
pour remplacer un terme de la forme
concat (concat t1 t2) t3parconcat t1 (concat t2 t3), vous pouvez combiner la tactiquerewriteavec le théorèmeconcat_associative:rewrite (concat_associative t1 t2 t3).
Utilisez maintenant le théorème thm_renverse_gen pour prouver
Theorem thm_renverse : forall l, renverse l = concat_renverse l [].
Pour cela, vous devrez :
-
utilisez
thm_renverse_genavec la tactiquerewritepour remplacerrenverse_concat l []parconcat (renverse l) [], -
utiliser
concat_vide_droiteet la tactiquesymmetry.qui remplace un butu=vpar le butv=u.

