Consignes

La collaboration orale est encouragée, mais le partage de code et le copier/coller (via Discord, github, etc.) n'est pas autorisé et pourra être pénalisé.

Le rendu de ce TP se fera uniquement par TPLab et consistera en une archive (zip, tar, etc.) contenant un répertoire TP2_NOM avec au minimum :

Vous pouvez ajouter d'autres fichiers s'ils sont documentés dans votre fichier README.txt.

Vous aurez compris que NOM devra être remplacé par votre nom (ou vos noms en cas de binômes) !

Tous vos fichiers doivent comporter une entête avec votre nom et votre groupe de TP.

Tout non respect d'une ou plusieurs de ces consignes entrainera automatiquement un retrait de points sur votre note !

Liens utiles

1. Algorithme de Dijsktra

1.1. Rappels : graphe pondéré

Le parcours en largeur permet de trouver le plus court chemin dans un graphe, lorsqu'on compte le nombre d'arêtes. Il ne fonctionne pas lorsque les arêtes ne sont pas toutes équivalentes, comme le montre l'exemple suivant :

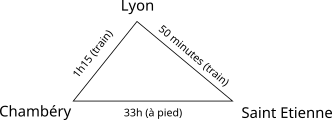
./TP2/Images/graphe-1.png

Un parcours en largeur trouvera un chemin de longueur 1 pour aller de Chambéry à Saint Etienne, mais la durée correspondante est loin d'être optimale.

On parle de graphe pondéré lorsque les arêtes ont un poids associé.

Le fichier graph.py est une variante de celui du TP qui gère les graphes pondérés. Les listes d'adjacence contiennent des paires (poids, voisin) au lieu de voisins simples. On peut donc parcourir les voisins du sommet s avec 

    for p, v in G[s]:
        ...

  1. Écrivez dans le fichier shortest_ALONZO.py une fonction max_out qui prend un graphe G en argument et renvoie le sommet dont la somme des poids sortants est maximale.

    Pour tester cette fonction, la complétez la fonction main_test pour qu'elle appelle la fonction max_out et affiche le résultat.

    Vous pourrez testez en donnant l'option -T sur la ligne de commande 

    $ python3 ./shortest_ALONZO.py -T graph_examples/graph1.txt
fonction main_test
le graphe contient 3 sommets
le sommet avec flot sortant max est : 1

  2. Écrivez également une fonction path_weight qui prend en argument un graphe G et une liste de sommets P. Votre fonction devra renvoyer la somme des poids des arêtes du chemin défini par P.

    Si les sommets de P ne forment pas un chemin, la fonction devra renvoyer None.

    Vous pouvez tester la fonction en décommentant la fin de la fonction main_test : 

    $ python3 ./shortest_ALONZO.py -T graph_examples/graph1.txt 0 1 2 0
fonction main_test
le graphe contient 3 sommets
flot sortant max d'un sommet du graphe : 2055.0
le chemin a un poids total de 2105.0

N'hésitez pas à utiliser la fonction main_test pour faire d'autres tests au cours du TP.

1.2. Plus court chemin : algorithme de Dijkstra

Échauffement : parcours en largeur

  1. Dans le fichier shortest-ALONZO.py écrivez une fonction BFS(G, v0, v1) qui fait un parcours en largeur du graphe G et qui s'arrête lorsqu'elle rencontre v1.

    Cette fonction ressemble beaucoup à la fonction BFS (ou BFS_opt si vous préférez cette version) du TP 1 car le poids des arêtes n'est pas utilisé pour le choix des sommets visités.

    En plus du tableau Pred (comme dans le TP 1), la fonction BFS doit également renvoyer un tableau D contenant les poids des chemins de v0 aux sommets parcourus. Pour calculer ce tableau D, il suffit

    • d'initialiser D[v0] à 0 et D[s] = ∞ pour tous les autres sommets. (On suppose que tous les poids sont des flottants. La constante oo définie dans le fichier shortest-ALONZO.py est justement le flottant +∞.)

    • de modifier D[v] lorsqu'on définit son prédécesseur : si Pred[v] = s, alors D[v] = D[s] + d lorsque d est le poids de l'arête de s vers v.

    Pour tester, vous pouvez lancer la commande suivante : 

    $ python3 ./shortest_ALONZO.py -A BFS graph_examples/graph2.txt
found path of weight 4.5580891922215 from 0 to 19

    Par défaut, le parcours est appelé avec v0=0 et v1=N-1. Vous pouvez changer ceci avec les options --start et --end: 

    $ python3 ./shortest_ALONZO.py -A BFS --start=7 --end=12 graph_examples/graph2.txt
found path of weight 11.649078967534761 from 7 to 12

    Suivant le parcours en largeur que vous avez implémenté, les valeurs peuvent changer.

  2. Le poids calculé dans le tableau D correspond il à la plus petite distance depuis v0 ?

Algorithme de Dijkstra

Comme le parcours en largeur, l'algorithme de Dijkstra peut se reconstruire à partir du parcours en profondeur basique, avec les modifications suivantes.

  1. Écrivez la fonction extract_best(ATraiter, D) qui recherche le sommet de ATraiter avec une valeur dans D minimale. La fonction devra renvoyer le sommet trouvé et le supprimer dans le tableau ATraiter.

  2. Écrivez la fonction shortest_path0(G, v0, v1) qui implémente l'algorithme décrit ci dessus. Vous pouvez partir de la fonction DFS du TP 1 et la modifier en ajoutant le tableau D et la gestion des voisins. (Vous devrez également remplacer l'appel s = ATraiter.pop() par un appel à la fonction extract_best.)

    Attention, on ne met Pred et D à jour que lorsque la nouvelle valeur de D[v] est meilleure (strictement plus petite) que l'ancienne.

    Vous pouvez appeler cet algorithme de parcours avec -A shortest_path0 : 

    $ python3 ./shortest_ALONZO.py -A shortest_path0 --start=9 --end=5 graph_examples/graph2.txt
found path of weight 6.0890260575204085 from 9 to 5

  3. Lorsque tous les poids sont égaux à 1.0, l'algorithme de Dijkstra et le parcours en largeur doivent donner des chemins de même poids. Vérifiez sur des exemples.

    Vous pouvez générer des graphes aléatoires avec la commande 

    $ python3 ./shortest_ALONZO.py --random-graph N D 1.0

    qui génèrera un graphe à N sommets, où pour chaque sommet, D voisins ont été tirés aléatoirement. Vous pouvez sauvez le résultat dans un fichier et le réutiliser dans la suite : 

    $ python3 ./shortest_ALONZO.py --random-graph 200 2 1.0 > test-graph.txt
$ python3 ./shortest_ALONZO.py -A BFS,shortest_path0  test-graph.txt
...

  4. Comparez les vitesses d'exécution des 2 algorithmes sur de gros graphes aléatoires.

  5. En utilisant le profiler intégré de Python, chercher d'où vient la différence de temps de calcul entre BFS et shortest_path0.

    Rappel : vous pouvez lancer un script Python en mode "profiling" avec 

    $ python3 -m cProfile -s tottime shortest_ALONZO.py ...
...

    Attention, l'exécution du script est plus lente lorsqu'il est exécuté en mode "profiling".

    Si vous n'avez pas le module cProfile, vous pouvez essayer avec -m profile.

1.3. De l'intérêt de l'algorithmique : file de priorité

Les files de priorités sont une structure de données avec les opérations suivantes :

Le module heapq de la librairie standard de Python offre une implémentation de cette structure de données en Python.

Nous voulons utiliser cette structure pour insérer des sommets avec une distance, et rechercher / supprimer l'élément de distance minimale. Il suffit d'utiliser une file de priorité avec des paires (distance, sommet). (Ça marche car l'ordre sur les paires est l'ordre lexicographique.)

L'exemple suivant montre comment créer une file de priorité, y insérer les sommet 0, 2 et 1 avec des distances arbitraires, et récupérer l'élément de distance minimale : 

$ python3
>>> from heapq import heapify, heappush, heappop

>>> ATraiter = []
>>> heapify(ATraiter)

>>> heappush(ATraiter, (78.5, 0))
>>> heappush(ATraiter, (3.7, 2))
>>> heappush(ATraiter, (123.0, 1))

>>> heappop(ATraiter)
(3.7, 2)
>>> heappop(ATraiter)
(78.7, 2)
>>> heappop(ATraiter)
(123.0, 1)

Attention, il ne faut pas oublier d'insérer les sommets avec leur priorité : heappush(ATraiter, (PRIORITÉ, SOMMET)).

  1. Écrivez la fonction shortest_path_dijkstra(G, v0, v1) en reprenant le code de shortest_path0, mais en utilisant une file de priorité.

  2. Vérifiez que les 2 fonctions donnent bien le même résultat sur des graphes aléatoires.

  3. Comparez l'efficacité des fonctions BFS, shortest_path0 et shortest_path_dijkstra sur des gros graphes, et en utilisant le profiler de Python.

2. Interlude : application au "recadrage intelligent" d'image

2.1. Description du problème

Une application surprenante de l'algorithme de Dijkstra est le "recadrage intelligent" d'images" ("seam carving" en anglais).

Le problème est le suivant : comment rétrécir une image (changer la largeur sans changer la hauteur), sans la déformer ?

Les méthodes naïves transforment l'image de gauche, en l'image de droite :

./TP2/Images/people-small.png ./TP2/Images/people-small-scaled.png

Les bulles ne sont plus rondes, et le garçon est déformé par la transformation.

L'objectif est d'obtenir l'image suivante, plus fidèle à la "réalité". (Passez la souris sur l'image pour visualiser la différence.)

L'idée est assez simple : pour passer de l'image originale (375x250) à l'image finale (250x250), 125 "chemins" ont été supprimés. L'image passe donc par des étapes intérmédiaires de tailles (374x250), (373x250), ...

Voici 2 exemples de chemins supprimés, visualisés en rouge :

./TP2/Images/people-small-000-seam.png ./TP2/Images/people-small-116-seam.png
étape 1 étape 116

Chaque chemin est une suite de pixel de l'image, un par ligne, qui se touchent. À chaque étape, nous supprimons le chemin de "poids" minimal, que l'on trouve ... en utilisant l'algorithme de Dijkstra.

Visuellement, la transformation ressemble à

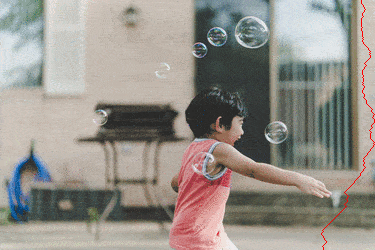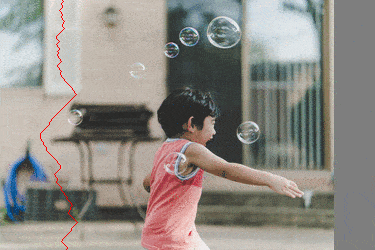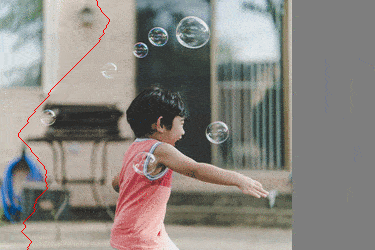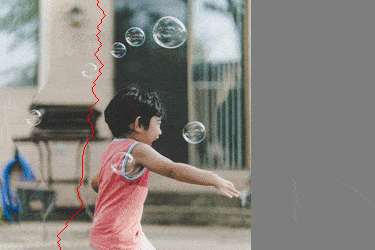
./TP2/Images/people-small.gif

On voit bien que les chemins choisis évitent les parties "saillantes" de l'images.

  1. Ce type de manipulation d'image est assez gourmand en ressources et Python n'est pas le langage le plus approprié.

    Le recadrage de l'image ci dessus a pris environ 25 secondes sur mon vieux portable, et 3 minutes 40 secondes pour la version 750x500 pixels ! Un langage compilé serait de loin préférable.

  2. Attention, les images présentes sur la page du sujet sont au format .png par soucis de compatibilité avec les navigateurs. Pour tester votre code, vous devrez utilisez des images au format .ppm comme celles présentes dans le répertoire Images de l'archive du TP.

  3. Si vous voulez tester sur d'autres images que celles fournies, il faudra les convertir au format .ppm. Si vous êtes sous Linux, l'utilitaire convert (du paquet imagemagick sous Debian / Ubuntu / ...) permet de le faire facilement : 

    $ convert MON_IMAGE -resize 300x300 RESULTAT.ppm

    convertira l'image du fichier MON_IMAGE (au format, .jpg, .png, etc.) au format .ppm et la redimensionnera pour qu'elle tienne dans un carré de 300 pixels de large. Le résultat sera sauvegardé dans le fichier RESULTAT.ppm.

  4. Pour visualiser les images .ppm, vous pouvez utiliser la commande display. (Elle fait partie du paquet imagemagick.) 

    $ display IMAGE1 IMAGE2 ...

Voici quelques exemples supplémentaires :

image originale après recadrage
./TP2/Images/lighthouse-small.png
./TP2/Images/soap-bubbles-small.png
./TP2/Images/family-small.png
./TP2/Images/gulls-small.png

2.2. Détails

Le fichier fourni construit un graphe à partir d'une image en reliant chaque pixel aux 3 pixels qui le touchent sur la ligne suivante.

./TP2/Images/pixels.png

De manière surprenante, dans cette version, le poids d'une arête (x,y) → (x', y'), ne dépend que du pixel d'arrivée (x',y').

Les pixels avec des voisins similaires sont associés à un petit poids : ce sont ceux qui se "fondent" dans leur voisinage et que l'on peut supprimer sans provoquer de discontinuité dans l'image.

L'objectif est de trouver le chemin de poids minimal entre un pixel de la première ligne (y=0) et un pixel de la dernière ligne (y=HAUTEUR-1).

Vous n'avez pas à calculer ces poids, mais pour les curieux, le poids associé aux pixel (x,y) est égal à

|P[x-1,y]-P[x+1,y]| + |P[x,y-1]-P[x,y+1]|.

On calcule la somme de la distance entre les pixels au dessus et au dessous (premier terme de la somme) et celle entre les pixels à droite et à gauche (second terme de la somme).

Les pixels avec un poids élevé (en blanc ci dessous) sont les pixels de "transitions" entre parties similaires de l'image :

./TP2/Images/people-small-energy.png

L'algorithme de Dijkstra évitera le plus possible ces pixels blancs car ils correspondent à des arêtes de poids élevé.

Complétez la fonction find_seam(img) qui utilise l'algorithme de Dijkstra pour chercher le chemin de poids minimal dans l'image img. La fonction doit renvoyer une paire S, e où

Le chemin S peut être extrait de l'arbre Pred calculé par l'algorithme de Dijkstra.

  1. L'argument img de find_seam du fichier seam_carving_ALONZO.py est une image. Vous aurez besoin

    • de sa taille, accessible avec img.width et img.height

    • de l'énergie associée à un pixel x,y, accessible avec img.E[y][x]. C'est avec ça qu'on calcule le poids d'une arête ? ⟶ (x,y).

    La valeur oo définit au début de la fonction est l'énergie maximale possible d'un chemin. Elle peut servir de valeur "infinie" pour les pixels non encore atteints.

  2. Pour simplifier le code, manipulez les sommets du graphe implicite comme des paires de coordonnées (x,y) plutôt que comme des entiers. Cela vous évitera de faire des conversions entre les 2 représentations. Pour cela, vous devrez donc :

    • utiliser un dictionnaire Pred pour associer les coordonnées du pixel précédent à un nouveau pixel,

    • utiliser un ensemble Vu contenant les coordonnées de pixels déjà rencontrés,

      Vous pouvez initialiser Vu avec Vu = set() et y ajouter des pixels avec Vu.add((x, y)).

    • utiliser un dictionnaire D pour enregistrer la plus petite distance trouvée pour chaque pixel. Lorsqu'un pixel n'est pas dans le dictionnaire, la distance associé est simplement oo. (Vous pouvez utiliser la méthode .get des dictionnaires pour faire cette opération facilement.)

    La file de priorité ATraiter reste une file de priorité. Elle contiendra des triplets (energie, x, y).

  3. Attention, comme il y a plusieurs sommets de départ possible (tous ceux de la première ligne), l'initialisation de Vu, D et ATraiter sera légèrement plus complexe que dans la version de l'algorithme de Dijkstra de la partie précédente.

    D'autre part, l'algorithme devra s'arrêter dès qu'un pixel sur la dernière ligne est rencontré.

  4. Pour tester, vous pouvez lancer la commande 

    $ python3 ./seam_carving_ALONZO.py IMAGE [NB]

    IMAGE doit être un fichier image au format .ppm, pas trop gros. Vous trouverez quelques exemples dans l'archive du TP (répertoire Images).

    Vous pouvez précisez le nombre de chemins à supprimer avec l'argument NB. Vous obtiendrez alors un fichier IMAGE-carved.ppm contenant le résultat.

    Si vous ne donnez pas l'argument NB, un seul chemin sera supprimé et vous obtiendrez un fichier supplémentaire IMAGE-000-seam.ppm contenant l'image originale avec le chemin trouvé en rouge.

    Voici quelques exemples de chemins trouvés à la première étape :

    ./TP2/Images/family-small-000-seam.png ./TP2/Images/gulls-small-000-seam.png ./TP2/Images/soap-bubbles-small-000-seam.png
    fichier family-small.ppm fichier gulls-small.ppm fichier soap-bubbles-small.ppm

Sur certaines images, il y a de nombreux chemins de poids minimal. Si on supprime le premier (plus à gauche), le résultat est "tassé sur la gauche" :

./TP2/Images/back-to-school-small.png ./TP2/Images/back-to-school-small-carved-1.png

Décrivez et implémentez une manière d'obtenir un résultat plus "équilibré" sur ce type d'images :

Il y a de nombreuses manières d'améliorer et de généraliser cette méthode.

  1. On peut utiliser une meilleure fonction de poids pour les chemins ("forward energy").

  2. On peut utiliser un masque sur l'image pour donner des poids très élevés à certaines zones. Cela permet de garantir qu'on ne les modifiera pas.

  3. On peut aussi utiliser un masque sur l'image pour donner des poids très faibles à certaines zones. Cela permet de supprimer certaines parties de l'image ! (Vous aviez vu que le garçon sur la plage avait disparu ?)

  4. On peut améliorer la recherche des chemins. Lorsqu'on supprime un chemin, une grande partie des calculs faits peut être réutilisée. (On verra une technique similaire dans le TP3.)

  5. On peut utiliser les chemins de poids minimal pour augmenter la largeur d'un pixel : on insère un chemin à gauche (ou à droite) du chemin minimal en prenant la moyenne des pixels de droite et de gauche. (Il y a une petite subtilité si on veut faire ça plusieurs fois...)

3. Plus court chemin avec heuristiques : A*

L'algorithme de Dijkstra choisit à chaque étape le sommet avec D[s] minimal. Lorsque tous les poids sont identiques, cela revient à faire un parcours en largeur car on commence par v0 (D[v0]=0), puis on passe aux voisins de v0 (D[s]=1), puis les voisins des voisins de v0 (D[s]=2), etc.

On peut ainsi calculer la distance de v0 à tous les autres sommets avec un seul parcours.

Un désavantage de cette méthode est que lorsqu'on est uniquement intéressé par la distance entre v0 et un sommet particulier v1, l'algorithme de Dijkstra ou le parcours en largeur explorent de nombreux sommets "inutiles" avant d'atteindre v1.

Dans certains cas, on peut estimer la "direction" de v1 et se concentrer sur les sommets qui nous "rapprochent" de v1.

Nous allons regarder 2 algorithmes de ce style :

3.1. "Best-first search" sur une grille

Nous allons reconsidérer des graphes provenant d'une grille carrée, du style 

..###...##..#.#..#....#..##
..#.#.##..#......#..#...#.#
.#...#..#.....#....#.......
#.#.#.##....#....##.##.....
.........#.......#.#..#..##
.#........##...#..##..#....
#..##.#...#.#..##...#.#.#..
......#.....#.....#...#.#..
#......#..#.#........#..##.
##..#...#...#.....#.#......
..........................#
..........###.....#....#.##
#.........#..##......#.....
......#.......#..#....#....
...##...#.........##.#.....

Les cases . sont libres, et les cases # sont occupées : chaque case a donc entre 0 et 4 voisines disponibles. (Les déplacements en diagonal ne sont pas autorisés.)

Les labyrinthes du TP1 peuvent être vu comme de telles grilles : 

#####################
#.#...#.............#
#.#.#.#.#########.#.#
#...#.......#...#.#.#
#.#########.###.#.#.#
#...#...#.#.....#.#.#
#.###.#.#.#.#####.#.#
#.#...#.#...#.....#.#
#.#.###.#####.#####.#
#.#...#.......#.....#
#####################

À la différence des premiers labyrinthes du TP 1 où seuls les caractères à coordonnées impaires étaient des sommets de graphe, tous les caractères sont bien des sommets.

Ces graphes ressemblent donc plus aux graphes de la seconde partie du TP 1.

Le parcours "best first search" est basé sur le parcours en profondeur basique. Le sommet s extrait de ATraiter est celui qui nous rapproche le plus du but à atteindre.

Comme la distance au but est inconnue (il faudrait faire un parcours de graphe pour la connaitre exactement), on l'approxime par une distance connue et facile à calculer : la distance au but si on suppose qu'il n'y a pas d'obstacle.

  1. Si s et v sont 2 sommets d'une grille G, comment peut-on calculer (en O(1)) la distance sans obstacle entre s et v. (Note : vous pouvez récupérer les coordonnées d'un sommet v avec G.xy(v).)

  2. Programmez la fonction best_first_search(G, v0, v1) qui cherche un chemin de v0 à v1 en commençant par les sommets qui "se rapprochent" de v1.

    Comme pour le parcours en largeur de la première partie, calculez également le tableau D donnant la distance (qui tient compte des poids des arêtes) des chemins explorés avec Pred.

  3. Comparez l'efficacité (en temps) du parcours en largeur usuel (partie 1) et ce nouveau parcours sur des grilles de tailles différentes.

    1. Vous pouvez générer des grilles aléatoires avec l'option --random-grid. Vous devrez préciser la largeur et hauteur, et ls proportions relatives des cases. Par exemples : 

      $ python3 ./shortest_ALONZO.py --random-grid 20 10 "....#"
...

      va générer une grille de largeur 20 et hauteur 10, où il y a environ 4 fois plus de . que de #.

    2. Vous pouvez rediriger la grille dans un fichier avec une redirection, et l'utiliser comme un fichier de graphe standard : 

      $ python3 ./shortest_ALONZO.py --random-grid 20 10 "....#" > ma_grille.txt
$ python3 ./shortest_ALONZO.py -A best_first_search --start=15,7 --end=19,9 ma_grille.txt
found path of weight 12 from 155 to 199
######################
#                    #
#                    #
#                    #
#                    #
#                    #
#                    #
#               ..   #
#              #@*#..#
#               .****#
#                ..#$#
######################

      Notes :

      • les caractères * correspondent aux cases du chemin trouvé par l'algorithme,

      • les arêtes ont un poids de 2, ce qui explique le poids total affiché (12),

      • les cases vides (espace) correspondent aux cases non explorées par l'algorithme.

  4. Pouvez vous construire des grilles où le parcours "best first search" a une meilleure complexité (en temps) que le parcours en largeur ?

3.2. Des grilles plus complexes

On place maintenant des tapis roulants sur certaines cases :

Les cases . sont toujours des cases vides, et les # des cases inaccessibles.

Les cases >, <, v et ^ aident les déplacements dans leur direction et entravent les déplacements dans la direction opposée. L'énergie nécessaire pour un changement de case est calculé comme suit :

case de départ vers la droite vers la gauche vers le haut vers le bas
> 1 4 3 3
< 4 1 3 3
v 3 3 4 1
^ 3 3 1 4
. 2 2 2 2

L'objectif est de trouver un chemin de cout minimal pour aller d'une case à une autre. Par exemple, pour la grille suivante (fichier grid_examples/grid-1.txt) 

v.>vv
^<^>>
v>^v>
^v.>.
.vv.<

il existe une solution de poids 14 pour aller du coin au haut à gauche au coins en bas à droite : 

$ python3 ./shortest_ALONZO.py -A shortest_path_dijkstra --start 0,0 --end 4,4 ./grid_examples/grid-1.txt
found path of weight 14 from 0 to 24
#######
#@***v#
#^<^*>#
#v>^*>#
#^v.**#
#.vv.$#
#######

Pour aller du coin en bas à droite au coin en haut à gauche, le meilleurs chemin à un poids de 15 : 

$ python3 ./shortest_ALONZO.py -A shortest_path_dijkstra --start 4,4 --end 0,0 ./grid_examples/grid-1.txt
found path of weight 15 from 24 to 0
#######
#$.>vv#
#***>>#
#v>**>#
#^v.*.#
#.vv*@#
#######

Lors de l'affichage des solutions :

  1. Vérifiez que votre fonction shortest_path_disjkstra donne le bon résultat.

  2. Quels sont les poids des chemins trouvés par BFS et best_first_search. Expliquez avec des mots d'où viennent les différences.

3.3. Algorithme A*

L'algorithme "best first search" choisit toujours le sommet le plus proche du but pour la fonction de distance approchée. Pour copier l'algorithme de Dijkstra et espérer trouver un chemin optimal, l'algorithme A* choisit le sommet s qui minimise D[s] + h(s):

  1. Codez la fonction a_star(G, v0, v1).

  2. Vérifiez qu'elle trouve un chemin optimal en comparant son résultat avec celui de shortest_path_dijkstra.

  3. En utilisant le profileur de Python, comparer l'efficacité de shortest_path_dijkstra et a_star.

Vous pouvez générer des grilles aléatoires avec l'option --random-grid. Par exemple : 

$ python3 ./shortest_ALONZO.py --random-grid 30 10 ".<>v^"
...

génère une grille 30x10 où les cases sont aléatoirement choisies parmi .<>v^. Pour obtenir une grille avec quelques obstacles, beaucoup des cases libre et des tapis roulants, on pourrait exécuter : 

$ python3 ./shortest_ALONZO.py --random-grid 30 10 ".....<>v^#"
...

3.4. A*, approximation

On modifie maintenant le cout des déplacements. Si on est sur une case >, le cout d'aller vers la droite est 0. Il suffit effectivement d'attendre que le tapis nous dépose sur la case de droite.

Les poids sont

case de départ vers la droite vers la gauche vers le haut vers le bas
> 0 3 2 2
< 3 0 2 2
v 2 2 3 0
^ 2 2 0 3
. 1 1 1 1

Vous pouvez changer les poids du graphe associé à une grille avec l'option --weights="a,b,c,d" :

La partie précédente utilisait implicitement l'option --weights="1,2,3,4", et il faut maintenant utiliser --weights="0,1,2,3".

  1. Comparez l'efficacité (en temps) de shortest_path_dijkstra, best_first_search et a_star dans ce cas. Qu'en pensez vous ?

  2. Quelle est la propriété importante de la distance approchée qui n'est plus vérifiée et qui fait que A* ne donne plus la réponse optimale ?

  3. Voyez vous des raisons d'utiliser A* (par rapport à shortest_path_dijkstra) dans ce cas ?