Support
Plans des kaléidoscopes
Envoyez moi des photos si vous construisez de tels kaleidoscopes !
Références
Livres et articles
-
John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things, AK Peters, 2008
-
Frank A. Farris, Creating Symmetry, the artful mathematics of wallpaper patterns, Princeton University Press, 2012
-
Martin Gardner, Extraordinary non-periodic tiling that enriches the theory of tiles, Scientific American, janvier 1977 (n° 236, pages 110--121)
reproduit dans Penrose Tiles to Trapdoor Ciphers, W.H.Freeman & Co Ltd, 1989
disponible en ligne http://www.maa.org/sites/default/files/pdf/pubs/focus/Gardner_PenroseTilings1-1977.pdf
-
Jean-Paul Delahaye, La quête du pavé apériodique unique, Pour la science, novembre 2013 (n° 240)
disponible en ligne http://www.lifl.fr/~jdelahay/pls/2013/240.pdf
-
Jean-Paul Delahaye, Les pavages pentagonaux: une classification qui s'améliore, Pour la science, octobre 2013 (n° 239),
disponible en ligne http://www.lifl.fr/~jdelahay/pls/2013/239.pdf
Sites divers
-
Kenneth G. Libbrecht, professeur de physique au California Institute of technology (Caltech), spécialiste des flocons de neige
-
"kaleidoscope mirror designs", avec des explications et de nombreuses photos de kaléidoscopes, dont des kaléidoscopes sphériques
-
Mark Newbold's POV-Ray Kaleidoscopes, point de départ pour la générations d'images de kaléidoscopes virtuels
Images
Frises
| 22∞ |

|
| ... |

|
| 2*∞ |

|
| ... |

|
| ∞× |

|
| ... |

|
| ∞∞ |

|
| ... |

|
| ∞* |

|
| ... |

|
| *22∞ |

|
| ... |

|
| *∞∞ |

|
| ... |

|
Pavages périodiques du plan
Les images suivantes ont été générées avec le programme create_symmetry.
Rotations pures

|

|

|

|
| 2222 ditropique | 442 quadritropique | ||

|

|

|
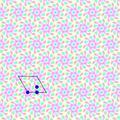
|
| 333 tritropique | 632 hexatropique | ||
Réflexions pures

|

|

|

|
| *2222 discopique | *442 quadriscopique | ||

|

|

|

|
| *333 triscopique | *632 hexascopique | ||
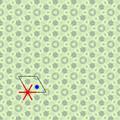
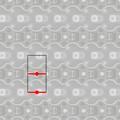
Mixte

|

|

|
|
| 2*22 dirhombique | 22* digyro | ||

|

|

|
|
| 4*2 tetragyro | 3*3 trigyro | ||
Autres

|
|

|
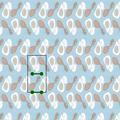
|
| ** monoscopique | ×× monoglisse | ||

|

|

|
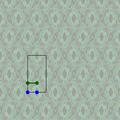
|
| *× monorhombique | 22× diglisse | ||
Le dernier
Ce motif n'est invariant par aucune symétrie en plus des deux translations.

|

|
| o monotropique | |
Pavagages périodiques de la sphère
Les images suivantes ont été générées avec le programme create_symmetry.

|

|

|
| 332 | 432 | 532 |

|

|

|
| *332 | *432 | *532 |

|
| 3*2 |

|

|
| NN (N=5) | 22N (N=5) |

|

|
| *NN (N=5) | *22N (N=5) |

|

|

|
| 2*N (N=5) | N× (N=5) | N* (N=5) |
Kaléidoscopes
Les images suivantes ont été générées avec le programme povray.
La première image utilise des miroirs imparfaits avec perte de luminosité au fur et à mesure des réflexions, et la seconde image utilise des miroirs parfaits.
Rosaces

|

|
| *N• (N=7) | |
Plan

|

|

|

|
| *442 | *442 | ||

|

|

|

|
| *333 | 632 | ||
Sphère

|

|

|

|
| *332 | *432 | ||

|

|

|

|
| *532 | *22N (N=7) | ||
Exercices
Rosaces
Les 2 types de rosaces sont :
-
*N• pour les rosaces avec un point miroir N (mais pas de point miroir d'ordre supérieur à N),
-
N• pour les rosaces avec un centre de rotation d'ordre N (mais pas d'ordre supérieur à N), sans point miroir.
Pour rappel, un point miroir d'ordre N est l'intersection de N axes de réflexion. Le flocon de neige suivant a donc un point miroir d'ordre 6... (La photo originale a été prise par Kenneth G. Libbrecht)
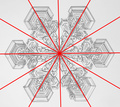
Reconnaitre les rosaces
Cherchez le type de rosaces des images suivantes...
|
|
|
|
|
|
|
|

|

|

|

|

|

|

|

|

|
Donnez le type de symétrie de chacune des lettres, minuscules et majuscules, ainsi que des chiffres...
a b c d e f g h i j k l m n o p q r s t u v w x y z A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 0 1 2 3 4 5 6 7 8 9
Fabriquer des rosaces
-
Si on plie une feuille en 2 et qu'on découpe un motif avant de la déplier, le résultat aura un axe de symétrie.
Est-il possible de plier une feuille pour obtenir des rosace de type *N• ?
-
Essayez de former un cône avec deux épaisseurs à partir d'une feuille comportant une demi-droite coupée. (Le sommet du cone sera le point de départ de la demi-droite.)
Découpez un motif le long du bord large du cône et dépliez le résultat. (Remarque : il est utile de scotcher le cone pour qu'il ne s'ouvre pas pendant la découpe...)
Quelle symétrie obtenez-vous ?
-
Est-il possible d'obtenir tous les types de symétries des rosaces en découpant une feuille de papier ?
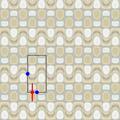
Frises
Fabriquer des frises
Essayez de fabriquer des frises en papier, en vous inspirant des ribambelles. Par ordre croissant de difficulté :
| code | frise | indice |
|---|---|---|
| *∞∞ |

|
accordéon |
| *22∞ |

|
... |
| ∞∞ |

|
roulé |
| ∞* |

|
... |
| ∞× |

|
ruban de Möbius |
Pouvez-vous imaginer une manière de plier / découper des frises avec les deux types de symétrie suivants ?
| code | frise |
|---|---|
| 22∞ |

|
| 2*∞ |

|
Plan
Essayer de reconnaitre le type de symétrie sur les photos suivantes.

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
... | ... |





