Consignes
La collaboration orale est encouragée, mais le partage de code et le copier/coller (via Discord, github, etc.) n'est pas autorisé et pourra être pénalisé.
Le rendu de ce TP se fera uniquement par TPLab et consistera en une archive (zip, tar, etc.) contenant un répertoire TP3-NOM avec au minimum :
-
vos fichiers maxflow-????_NOM.py,
-
un fichier README.txt contenant les réponses aux questions et vos remarques et observations.
Vous pouvez ajouter d'autres fichiers s'ils sont documentés dans votre fichier README.txt.
Vous aurez compris que NOM devra être remplacé par votre nom (ou vos noms en cas de binômes) !
Tous vos fichiers doivent comporter une entête avec votre nom et votre groupe de TP.
Tout non respect d'une ou plusieurs de ces consignes entrainera automatiquement un retrait de points sur votre note !
Liens utiles
-
archive du TP TP3_KURT.tar.gz, contenant le code (décrit plus bas) et des images pour tester
-
lien vers l'article original décrivant la méthode "Interactive Graph Cuts for Optimal Boundary & Region Segmentation of Objects in N-D Images"
-
lien vers l'article original décrivant les optimisations de l'algorithme Edmonds-Karp décrites dans la dernière partie du TP : l'algorithme de Boykov-Kolmogorov
1. Préliminaires
1.1. Segmentation
La segmentation d'image consiste à détecter des régions "uniformes" dans une image. On peut par exemple détecter des visages, des véhicules, des tumeurs, etc.
Nous allons implémenter une technique de segmentation basée sur un l'algorithme du flot maximum.
Il s'agit d'une segmentation "supervisée" : l'utilisateur commence par marquer certains pixels comme des pixels "fond" (en rouge) et d'autres comme des pixels "objet" (en vert). Le but est de classer les autres pixels comme "fond" ou "objet".
Voici un exemple :

|

|

|
| image initiale | marquage | image segmentée |
Plus l'utilisateur spécifie des pixels au départ, plus la segmentation sera précise et (en général) rapide. Voila quelques exemples de marquages successifs avec les temps de calcul sur mon ordinateur fixe, avec les choix par défaut et la première version "raisonnable" du code (maxflow-EK_KURT.c) :

|

|
| marquage | segmentation : 6 secondes |

|

|
| marquage | segmentation : 4 secondes |

|

|
| marquage | segmentation : 4 secondes |

|

|
| marquage | segmentation : 2 secondes |
La complexité de l'algorithme et la taille des graphes utilisés rendent Python inadapté. Pour éviter de commencer le TP par l'avertissement suivant :
Le programme ne devrait être utilisé que sur de toute petites images. Nous avons trouvé expérimentalement que le programme s'exécute en un temps raisonnable (moins de une minute) sur des images de taille 30x30. Toutes les images sont donc redimensionnées à cette taille au début du programme.
j'ai décidé de remplacer Python par C. En effet, segmenter l'image  pour obtenir
pour obtenir  n'est pas très amusant !
n'est pas très amusant !
1.2. Segmentation par recherche de flot maximal
Un algorithme de segmentation doit chercher une frontière entre plusieurs régions. Il est naturel de positionner cette frontière entre des pixels fortement différents.
Pour l'image suivante (fortement zoomée) de taille 10x1, si le pixel gauche (n° 0) fait partie du fond et le pixel droit (n° 9) fait partie de l'objet

|
la différence la plus grande possible se trouve entre les pixels 4 et 5 (transition blanc - noir), et c'est là qu'il est naturel de mettre la frontière.
L'idée est donc de chercher une frontière qui maximise les différences entre pixels, ou de manière équivalente, qui minimise les similarités entre pixels. Cela permet d'obtenir par exemple la segmentation suivante, où l'objet et le fond utilisent exactement les même couleurs.

|

|

|
| image initiale | marquage | image segmentée |
On associe donc un graphe à l'image à segmenter. Les sommets sont les pixels, avec des arêtes entre pixels voisins.
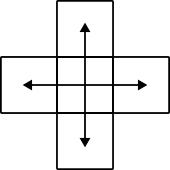
|
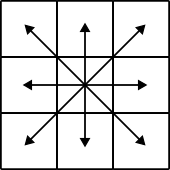
|
| 4 voisins (défaut) | 8 voisins (option -8) |
Les détails ne sont pas importants pour la suite (regardez la fonction
capacity_neightboors du fichier graph.c si ça vous intéresse), mais le poids d'une
arête mesure la similarité entre couleurs des pixels et les poids des arêtes
en diagonale (si on les utilise) est divisé par 1.4142 car les pixels
sont plus éloignés.
Rechercher la définition de coupe dans votre cours (ou sur wikipedia) et expliquez dans votre fichier README.txt (avec vos propres mots) pourquoi une segmentation s'apparente à une coupe de poids minimal dans le graphe décrit ci dessus.
1.3. Code fourni
L'archive du TP contient l'arborescence suivante :
T3_KURT
├── images
│ ├── ...
│ └── ...
└── src
├── Makefile
├── ...
├── graph.c
├── graph.h
├── maxflow-FFDFS_KURT.c
└── ...Le seul fichier que vous devez modifier est le fichier maxflow-FFDFS_KURT.c.
La structure de graphe
Le graphe construit à partir de l'image est stocké dans une structure de type
graph* représentant un graphe pondéré. En voici une définition
simplifiée
// arcs
typedef struct {
size_t target; // target of the arc
int capacity; // weight of the arc
arc *opposite; // NOTE: ce n'est pas du C valide
} arc;
// graph
typedef struct {
size_t nb_nodes; // number of nodes in the graph
size_t* degree; // degree[v] gives the degree of node v
arc** Adj; // Adj[v] is the array of neighboors of v, of // length degre[v]
// This array ends with an extra dummy arc with target == NULL_NODE
} graph;
(la définition complète se trouve dans le fichier graph.h. Vous pouvez ignorer les autres champs, qui n'ont qu'un rôle interne).
Notez bien les points suivants.
-
Tous les graphes / arêtes sont donnés par des pointeurs :
arc* aetgraph* G. -
Les sommets d'un graphe sont des entiers, du type
size_t. (Il faut utiliser%zupour les afficher dans unprintf.) -
Un graphe est représenté par ses listes d'adjacences
G->Adj, -
Si
Gest de typegraph*etsest un sommet,G->Adj[s]est le tableau des arêtes sortant des.La taille de ce tableau est
G->degree[s]. (En C, on ne peut pas calculer la taille d'un tableau, il faut la stocker quelque part). -
L'arête vers le deuxième voisin est donc
G->Adj[s][1]. Elle contient-
un champs
targetqui est le numéro du sommet voisin, -
un champs
capacityqui est la capacité de l'arête. -
Pour simplifier certaines parties du code, l'arête contient également un pointeur vers l'arête opposée.
-
-
Chaque tableau
G->Adj[s]contient en fait une case supplémentaire avec une arête bidon. Cette arête a son champstargetàNULL_NODEqui ne correspond à aucun sommet.
Pour faire une boucle sur les voisins d'un sommet s, on peut
donc faire une boucle jusqu'à G->degre[s] :
for (size_t i = 0; i < G->degree[n]; i++) {
arc a = G->Adj[n][i];
...
... a.target ... a.capacity ...
...
}
ou une boucle jusqu'à tomber sur l'arête bidon :
for (arc* a = G->Adj[from]; a->target != NULL_NODE; a++) {
...
... a->target ... a->capacity ...
...
}
Je vous conseille la seconde version qui a l'avantage de ne pas nécessiter de
variable supplémentaire i et de ne pas mélanger les
arc et les arc*. Vous n'aurez donc pas à réfléchir
quand utiliser a.target et quand utiliser
a->target.
-
En utilisant la description de la structure de graphe ci dessus, complétez la fonction
arc* get_arc(graph* G, size_t from, size_t to)du fichier maxflow-FFDFS_KURT.c.Cette fonction renvoie un pointeur vers la structure
arccorrespondant à l'arête qui va du sommetfromau sommetto.S'il n'y a pas d'arête de
fromàto, la fonction renverraNULL.Pour tester votre fonction, utilisez la fonction
main_testdu fichier maxflow-FFDFS_KURT.c. Cette fonction prend un graphe en argument (construit à partir d'une image comme décrit précédemment) ainsi que les arguments de la ligne de commande.Voici par exemple comment afficher la capacité d'une arête entre 2 sommets :
int main_test(graph* G, size_t argc, char* argv[]) { UNUSED(argc); // pour éviter le warning "unused argument" UNUSED(argv); // pour éviter le warning "unused argument" if (argc < 2) { ┆ printf("Il faut donner 2 sommets sur la ligne de commande !\n"); exit(2); } size_t v1 = atol(argv[0]); size_t v2 = atol(argv[1]); arc* a = get_arc(G, v1, v2); if (a == NULL) { printf("Les sommets %zu et %zu ne sont pas reliés.\n", v1, v2); } else { printf("L'arête entre %zu et %zu a un capacité de %i.\n", v1, v2, a->capacity); } return 0; }Pour appeler la fonction de test, il faut donner l'argument --test sur la ligne de commande. Vous devrez fournir les noms du fichier image et celui du fichier image annotée (...-seeds.ppm) pour construire le graphe.
$ make ... $ ./segment-FFDFS ../images/rose-small.ppm ../images/rose-small-seeds.ppm --test 207 432 L'arête entre 207 et 432 a un capacité de 9884. $ ./segment-FFDFS ../images/rose-small.ppm ../images/rose-small-seeds.ppm --test 307 432 Les sommets 307 et 432 ne sont pas reliés. -
Pour tester : en sachant que les sommets du graphe sont les pixels de l'image et sont numérotés de gauche à droite, puis de haut en bas,
-
vérifiez que dans le fichier images/rose-small.ppm, la capacité de l'arête du pixel 215 vers le pixel juste en dessous est de 9997.
-
cherchez la capacité de l'arête entre le pixel 39111 et le pixel 39336 et donnez le dans votre fichier README.txt.
-
Réseau de flot
Par le théorème coupe min / flot max évoqué en cours, donner une coupe de poids minimal est équivalent à donner un flot maximal. Mais pour cela, il faut s'assurer que le graphe des pixels est un réseau de flot. Il faut donc ajouter 2 sommets particuliers au graphe : la source et le puits.
Intuitivement, les pixels marqués en vert ("objet") sont des sources, et les sommets marqués en rouge ("fond") sont des puits. Pour obtenir un graphe avec une seule source et un seul puits, on ajoute 2 sommets :
-
un sommet s, relié à tous les pixels marqués en vert,
-
un sommet p, relié à tous les pixels marqués en rouge.
Pour une image 6x4 pixels, le graphe pourrait donc ressembler à
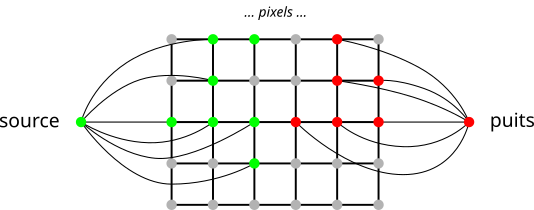
En plus de sa capacité, chaque arête a également un flot la traversant.
Le type graph contient ces informations :
-
le type
arca un champsflowde typeint, initialisé à0, -
la source et le puits d'un
Gde typegraph*sont accessibles avecG->sourceetG->sink.
-
Par construction, la capacité d'une arête est toujours égale à la capacité de l'arête opposée. Vous ne devez jamais modifier la capacité d'une arête.
-
Les flots d'une arête et de son opposée doivent toujours être opposés : si une arête a un flot de
37, son opposée doit avoir un flot de-37. Faites donc attention à toujours modifier le flot d'une arête en même temps que le flot de son opposée. -
D'autre part, le flot passant dans une arête ne doit jamais dépasser la capacité de l'arête.
-
Écrivez la fonction
int find_path(graph* G, size_t Pred[], int Seen[])qui fait un parcours en profondeur basique dans le graphe résiduel du flotGpour trouver un chemin de la source vers le puits.Consignes :
-
Pour le parcours, utilisez un parcours basique, c'est à dire le parcours en profondeur basique.
-
Les arguments
PredetSeen(appeléVudans les TP précédents) sont des tableaux alloués de tailleG->nb_nodes, mais non initialisés. Vous devez donc les réinitialiser au début de votre fonction. (Avec desNULL_NODEpourPred, et des0pourSeen.) -
Le point de départ n'est pas donné comme argument car c'est toujours
G->source. -
Seules les arêtes non saturées sont utilisables, c'est à dire les arêtes qui satisfont
a->flow < a->capacity. Il faut donc ajouter un test lorsqu'on regarde les voisins du sommet courant. -
Le parcours s'arrête dès que
G->sinkest rencontré, ou lorsque tout le graphe a été parcouru. La fonction doit renvoyer1dans le premier cas, et0sinon.
Vous aurez besoin d'une pile
todo(appeléeATraiterdans les TP précédents) contenant des sommets. Le typestack(défini dans le fichierstack.c) permet de faire ça :-
pour créer une nouvelle pile vide :
stack* todo = new_stack();, -
pour vérifier si la pile est vide
if (is_empty_stack(todo)) {...}, -
pour empiler un sommet
sdans la file :push_stack(todo, s);, -
pour dépiler le dernier élément et stocker le résultat dans la variable
v:pop_stack(todo, &v).
Attention, la fonction
pop_stack, de typeint destack(stack* Q, size_t* elem);ne renvoie pas l'élément. Elle stocke l'élément dépilé à l'adresseelemet renvoie1si ça a marché, et0si la pile était vide.Pour information, le code supprimé de la fonction
find_pathfait environ 22 lignes dont 2 lignes vides, 5 lignes réduites à}et 2 lignes de commentaires. -
-
Pour tester, vous pouvez modifier la fonction
main_testpour qu'elle-
alloue les tableaux
PredetSeenavecint* Seen = malloc(G->nb_nodes * sizeof(int)); size_t* Pred = malloc(G->nb_nodes * sizeof(size_t)); -
appelle la fonction
find_pathet affiche un message avec le résultat.
Vous devriez obtenir le résultat suivant :
$ ./segment-FFDFS ../images/disk-small.ppm ../images/disk-small-seeds.ppm --test Chemin trouvé ! 25602 sommets ont été vus pendant le parcours. $ ./segment-FFDFS ../images/harvest-small.ppm ../images/harvest-small-seeds.ppm --test Aucun chemin trouvé de la source vers le but ! -
-
Expliquez pourquoi il n'y a pas de chemin dans le réseau correspondant à l'image harvest-small.ppm avec les annotations harvest-small-seeds.ppm.
2. Recherche du flot maximal : algorithme de Ford-Fulkerson
Le principe de l'algorithme
de Ford-Fulkerson est simple : tant qu'on trouve un chemin (avec
find_path), on augmente le flot du réseau en utilisant ce chemin.
Petit à petit, le flot global du réseau augmente et des arêtes se saturent
(leur flot devient égal à leur capacité). Au bout d'un moment, la fonction
find_path échouera et on aura trouvé le flot maximal.
Il nous manque 2 étapes :
-
trouver le flot que l'on peut faire passer dans le chemin renvoyé par
find_path, -
augmenter le flot des arêtes de ce chemin.
2.1. Fonctions auxiliaires
-
Écrivez une fonction
int find_bottleneck(graph* G, const size_t Pred[])qui prend en argument un grapheGet un tableauPredcalculé parfind_path.En remontant dans le tableau
Pred, on peut remonter du puits deGjusqu'à la source deG.La fonction
find_bottleneckdoit renvoyer le plus grand flot que l'on peut faire passer par ce chemin dans la direction source ⟶ puits.-
Attention, à bien regarder l'arête qui va dans le bon sens, c'est à dire de
Pred[v]versv. -
le flot possible d'une arête est calculé dans le graphe résiduel. Pour l'arête
a, il s'agit dea->capacity - a->flow. -
Comme le flot doit être conservé le long du chemin, le meilleur flot que l'on peut faire passer à travers un chemin est le minimum des meilleurs flot que l'on peut faire passer sur ses arêtes.
Pour information, le corps de ma fonction
find_bottleneckfait environ 10 lignes dont 1 ligne réduite à}et la ligne finalereturn flow. -
-
Pour tester, vous pouvez utiliser la fonction de test suivante :
int* Seen = malloc(G->nb_nodes * sizeof(int)); int r = find_path(G, Pred, Seen); if (r == 0) { printf("Aucun chemin trouvé de la source au puits !\n"); } else { printf("Chemin trouvé !\n"); int flow = find_bottleneck(G, Pred); printf("Le flot maximal possible le long du chemin est de %i.\n", flow); } -
Vous devriez obtenir :
$ ./segment-FFDFS ../images/disk-small.ppm ../images/disk-small-seeds.ppm --test Chemin trouvé ! Le flot maximal possible le long du chemin est de 220. $ ./segment-FFDFS ../images/harvest-small.ppm ../images/harvest-small-seeds.ppm --test Aucun chemin trouvé de la source vers le but !
Une fois un chemin trouvé et le flot maximal admissible connu, on peut
augmenter le flot global du réseau G. Pour ceci, il suffit de
reparcourir le chemin de G->source à G->sink
et d'ajouter le flot à toutes les arêtes.
Complétez le code de la fonction void augment_flow(graph* G, const
size_t Pred[], int flow) pour faire ceci :
-
Gest le réseau avec un flot global courant (initialement,0partout), -
Predest le tableau calculé parfind_pathet contient donc un chemin deG->sourceversG->sink, -
flowest la valeur du flot qu'il faut ajouter aux arêtes.
Attention, lorsque vous ajoutez flow à une arête
a, il ne faut pas oublier de soustraire flow à
l'arête opposée !
La structure de cette fonction est très proche de la précédente.
-
find_bottleneckparcourt le chemin deG->sourceàG->sink(en partant deG->sink) pour trouver le flot résiduel minimal, -
augment_flowparcourt le chemin deG->sourceàG->sink(en partant deG->sink) pour augmenter le flot des arêtes.
Pour information, le corps de ma fonction augment_flow fait
environ 8 lignes dont 1 ligne réduite à }.
Pour tester lorsque la compilation réussie, vous pouvez ... passer à la question suivante.
2.2. Flot maximal et segmentation
Sans les messages de log, la fonction maxflow du fichier
maxflow-FFDFS_KURT.c a la forme
int maxflow(graph* G, int Seen[])
{
// allocate the Pred array
size_t* Pred = malloc(G->nb_nodes * sizeof(size_t));
int flow_counter = 0;
while (find_path(G, Pred, Seen)) {
int flow = find_bottleneck(G, Pred);
flow_counter += flow;
augment_flow(G, Pred, flow);
}
free(Pred);
return flow_counter;
}
Tant qu'il y a des chemins de la source vers le puits, on les utilise pour augmenter la valeur du flot global. Lorsque c'est fini, la fonction renvoie la valeur finale de ce flot.
Après le dernier appel à find_path (qui a échoué), le tableau
Seen contient la liste de tous les sommets rencontrés pendant le
parcours. Il donne donc la liste des sommets accessibles depuis
G->source dans le réseau saturé. Ce sont les sommets
correspondant aux pixels de l'objet et la fonction main le
récupère pour générer l'image résultat.
-
Vérifiez que le code compile et testez la fonction
maxflowen segmentant une image.$ ./segment-FFDFS ../images/rose-small > final flow value is 1241478 > resulting image saved to file '../images/rose-small-output.ppm' $ display ../images/rose-small-output.ppmNote : la segmentation prend environ 68 secondes sur mon ordinateur fixe. Vous pouvez utiliser l'image rose-tiny.ppm, plus petite, pour une segmentation plus rapide.
$ ./segment-FFDFS ../images/rose-tiny [14:14] +41 > final flow value is 198011 > resulting image saved to file '../images/rose-tiny-output.ppm'Vous pouvez afficher quelques messages supplémentaires avec l'option -v, et visualiser chaque appel à
find_pathavec l'option -vv. -
Expérimentez avec d'autres fichiers et documentez ce que vous observez.
-
Si vous ne donnez qu'un seul argument BASE à la commande segment-FFDFS (ici, "../images/rose-small"), le programme utilisera
-
BASE.ppm comme fichier image à segmenter (ici "../images/rose-small.ppm"),
-
BASE-seeds.ppm comme fichier d'annotations sur l'image (ici "../images/rose-small-seeds.ppm") ;
-
et le résultat sera sauvegardé dans le fichier BASE-output.ppm (ici "../images/rose-small-output.ppm").
Vous pouvez préciser les fichiers individuellement en donnant 3 arguments :
$ ./segment-FFDFS ../images/rose-small.ppm ../images/rose-small-seeds.ppm ../images/rose-small-output.ppm -
-
Le fichier contenant les annotations (comme ../images/rose-small-seeds.ppm) doit être un fichier .ppm de même taille que le fichier à segmenter. Les pixels verts (RGB = 0x00ff00) sont des pixels de l'objet et les pixels rouges (RGB = 0xff0000) sont des pixels du fond.
Le plus simple pour faire ces annotations est de convertir l'image originale en niveaux de gris avec la commande suivante :
$ convert flower.ppm -set colorspace Gray flower-seeds.ppmVous pouvez également utiliser le script prepare.sh présent dans le répertoire images. Ce script prend une image (dans un format quelconque) et une taille en argument. Il produit, dans le répertoire courant, un fichier .ppm de la taille demandée et un fichier d'annotations -seeds.ppm correspondant. Ce script nécessite d'avoir installé le paquet imagemagick (sudo apt install imagemagick sous Debian / Ubuntu).
Par exemple :
$ ../Images/prepare.sh /tmp/ma_photo.jpg 300x300 fichier ma_photo.ppm créé fichier ma_photo-seeds.ppm crééPour ajouter les annotations, vous pouvez utiliser n'importe quel logiciel de dessin avec support du format .ppm. (Gimp est installé sur les machines de l'université.)
-
3. Améliorations
3.1. Facile : utiliser un parcours en largeur (algorithme de Edmonds-Karp)
L'algorithme de Ford-Fulkerson ne précise pas quelle méthode utiliser pour chercher les chemins augmentants. L'algorithme de Edmonds-Karp est le cas particulier de Ford-Fulkerson où l'on utilise un parcours en largeur.
-
Copiez votre fichier maxflow-FFDFS_KURT.c sur maxflow-EK_KURT.c.
Ne modifiez plus maxflow-FFDFS_KURT.c, mais seulement maxflow-EK_KURT.c pour pouvoir les comparer. (La compilation génèrera plusieurs fichiers exécutables.)
-
Modifiez la chaine
VERSIONen haut du fichier pour préciser que le parcours utilisé est le parcours en largeur. -
Modifiez la fonction
find_pathpour transformer le parcours en profondeur basique en parcours en largeur basique :-
on utilise une file
todoplutôt qu'une pile -
on ne remet pas les voisins ayant déjà un prédécesseur dans
todo.
Vous aurez besoin d'une file
todocontenant des sommets. Le typequeue(défini dans le fichierqueue.c) permet de faire ça :-
pour créer une nouvelle file vide :
queue* todo = new_queue();, -
pour vérifier si la file est vide
if (is_empty_queue(todo)) {...}, -
pour enfiler un sommet
sdans la file :enqueue(todo, s);, -
pour défiler le premier élément et stocker le résultat dans la variable
v:dequeue(todo, &v).
Attention, la fonction
dequeue, de typeint dequeue(queue* Q, size_t* elem);ne renvoie pas l'élément. Elle stocke l'élément défilé à l'adresseelemet renvoie1si ça a marché, et0si la file était vide. -
-
Recompilez et comparez les temps d'exécution de segment-FFDFS et segment-EK sur plusieurs exemples.
N'oubliez pas de vérifier que les flots maximums trouvés sont identiques !
-
Essayez d'expliquer pourquoi la version avec le parcours en largeur est plus efficace que celle avec le parcours en profondeur.
3.2. Profilage
La segmentation d'une image prend du temps. Avec la version BFS, sur mon ordinateur fixe, la segmentation d'une image de taille 600x400 a pris environ 36 secondes. Ce temps n'est pas linéaire, et la segmentation de la même image de taille réduite à 50% (300x200) a pris moins de 1.5 seconde ! Ce temps dépend de la taille de l'image, des pixels de l'image, mais aussi des annotions données. (Pour info, la version DFS prenait respectivement 11 minutes et 15 secondes.)
L'objectif de la suite de la suite du TP est d'améliorer la vitesse de segmentation en optimisant le code et améliorant la partie algorithmique.
La segmentation de mon image de test avec maxflow-BK1_KURT.c (avant dernière question du TP) prend moins de 1 seconde.
En implémentant des optimisations supplémentaires "simples" (partie bonus de la dernière question), le temps de segmentation descend à 0.35 seconde, soit un facteur de gain de 100 par rapport à la version initiale !
Comme le langage C est un langage compilé, le profilage est légèrement plus complexe qu'avec Python. Pour profiler votre code, vous devez :
-
compiler avec les options -Og -pg (deuxième ligne
FLAGS = ...dans le fichier Makefile fourni), -
lancer le programme comme d'habitude (attention, c'est plus lent),
-
lancer la commande gprof sur l'exécutable pour afficher les statistiques.
$ make veryclean all
gcc -std=c99 -Wall -Wextra -pedantic -Werror -Wno-unused-parameter -Og -pg -c maxflow-EK_KURT.c
...
$ ./segment-EK ../images/rose-small
...
$ gprof ./segment-EK
Flat profile:
Each sample counts as 0.01 seconds.
% cumulative self self total
time seconds seconds calls s/call s/call name
44.22 1.22 1.22 1889 0.00 0.00 find_path
11.96 1.55 0.33 245675939 0.00 0.00 is_empty_stack
9.42 1.81 0.26 127493382 0.00 0.00 LOG
...
...-
Choisissez une image dont la segmentation prend quelques secondes en mode profilage.
Vous pouvez chronométrer le temps d'exécution d'une commande en ajoutant time au début de la ligne :
$ time ./segment-EK ../images/rose-small > final flow value is 1241478 > resulting image saved to file '../images/rose-small-output.ppm' 2.78user 0.00system 0:02.78elapsed 100%CPU (0avgtext+0avgdata 14168maxresident)k 0inputs+352outputs (0major+617minor)pagefaults 0swapsPour ajuster le temps, vous pouvez diminuer la taille de l'image, ou ajouter des annotations. Les annotations suivantes produisent exactement le même résultat :



15 secondes 8 secondes 3 secondes -
Faites le profilage de votre code comme décrit plus haut.
-
Pour éviter de parcourir deux fois le chemin augmentant, on pourrait supprimer la fonction
find_bottlenecket calculer le flow maximal admissible dans la fonctionfind_path, comme dans le TP 2. Il suffirait d'utiliser un tableauFcontenant le flot admissible pour aller deG->sourceà chaque sommet rencontré lors du parcours.(Au lieu de faire
D[v] = D[s]+poids, on feraitF[v] = min(F[s], capacity-flow).)À votre avis, est-ce que cette optimisation est intéressante ? Argumentez votre réponse.
Lorsqu'on utilise un chemin augmentant, on utilise la fonction
get_arc pour récupérer l'arête de Pred[v] vers
v. Cette fonction doit parcourir la liste des voisins de
Pred[v].
-
Que pensez vous de cette fonction sur les graphes utilisés dans ce TP ? À votre avis, est-ce qu'optimiser cette fonction est intéressant ? Profilez votre code pour vérifier.
-
Pour implémenter une optimisation possible, copiez votre fichier maxflow-EK_KURT.c dans maxflow-EK2_KURT.c, et remplacez le tableau
size_t Pred[]calculé parfind_pathpar un tableau d'arêtes*arc Pred[]. Vous pourrez ensuite modifier-
find_bottleneck(graph* G, arc* const Pred[]) -
et
augment_flow(graph* G, arc* const Pred[], int flow)
pour ne plus utiliser
get_arc.(Il faudra aussi changer l'initialisation de
Pred.) -
-
Testez et profilez votre code. Qu'en pensez vous ?
3.3. Moins facile : conserver les données de chaque parcours
Le passage du parcours en profondeur au parcours en largeur amène un gain de
temps non négligeable, mais il est possible de faire beaucoup mieux. L'idée
est la suivante : la fonction find_path est appelé de nombreuses
fois avant de trouver le flot maximal. À chaque fois, le parcours repart de
zéro. On peut espérer gagner du temps en réutilisant les calculs faits lors
des parcours précédents.
Ce genre de technique ne marche pas toujours car le temps passé à vérifier ce que l'on peut garder des calculs précédents peut être supérieur au temps nécessaire pour les refaire !
L'idée développé ici est la base de l'algorithme de Boykov-Kolmogorov, l'un des plus efficaces sur les graphes issus d'images comme ceux que nous manipulons. (Théoriquement, la complexité au pire cas est pourtant moins bonne !)
-
Il va falloir repartir du parcours en largeur : copier votre fichier maxflow-EK_KURT.c sur maxflow-BK0_KURT.c.
Ne modifier plus maxflow-FFDFS_KURT.c ou maxflow-EK_KURT.c, mais seulement maxflow-BK0_KURT.c pour pouvoir les comparer.
-
Modifiez la chaine
VERSIONen haut du fichier pour préciser que le parcours utilisé est le parcours en largeur basique avec une réutilisation des calculs. -
La file
todoest réallouée à chaque appel à la fonctionfind_path. Déclarez la dans la fonctionmaxflowet passez la comme argument defind_pathqui aura donc le prototypeint find_path(graph* G, size_t Pred[], int Seen[], queue* todo). (N'oubliez pas de déplacer aussi sa désalocation (free_queue(todo)) dans la fonctionmaxflow.)Au lieu de la déclarer, la fonction
find_pathaura simplement besoin de la remettre à zéro avec un appel àempty_queue(todo). -
Vérifiez que votre code compile et donne des résultats cohérents avant de passer à la suite. Le temps de calcul ne devrait pas changer significativement.
Mise à jour du tableau Pred
À la fin de la fonction find_path, le tableau Pred
contient un arbre enraciné sur G->source. Si l'appel à réussi,
cet arbre contient G->sink. Visuellement, ça pourrait
ressembler à :
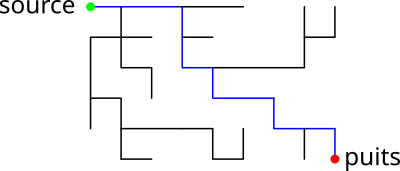
Lorsqu'on augmente le flot global du réseau avec ce chemin, au moins une des
arêtes de l'arbre devient saturée (a->capacity ==
a->flow) : on ne peut plus augmenter le flot sur cette arête.
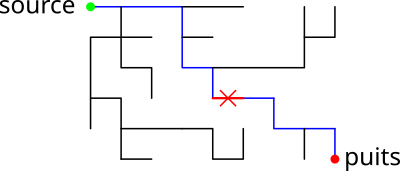
On peut conserver l'arbre calculé dans Pred à condition de
supprimer les sommets qui ne sont plus rattachés à l'arbre : les "orphelins".
On obtiendrait donc l'arbre suivant.
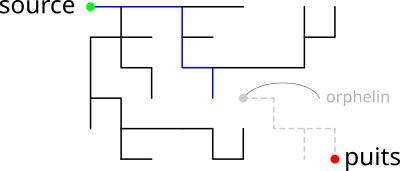
-
Modifiez la fonction
augment_flowpour qu'elle calcule la liste des orphelins créés et les déconnecte de l'arbrePred.Cette liste sera en fait une pile (type
stack) qui sera passée en argument. Vous pourrez y ajouter des sommets avec la fonctionpush.void augment_flow(graph* G, size_t Pred[], int flow, stack* orphan) { ... // s est un orphelin push(orphan, s); Pred[s] = NULL_NODE; ... } -
Ajoutez, dans la fonction
maxflow, l'initialisation de la pile des orphelins, et sa désalocation :int maxflow(graph* G, int Seen[]) { stack* orphan = new_stack(); ... augment_flow(G, Pred, flow, orphan); ... free_stack(orphan); return flow_counter; } -
Vérifiez que le code compile et donne des résultats cohérents. (Il ne devrait pas y avoir de différence de temps d'exécution car rien n'a encore été fait pour garder l'arbre
Pred.) -
Complétez le code de la fonction
void update_Pred(graph* G, size_t Pred[], queue* todo, int Seen[], stack* orphan)qui doit déconnecter tous les descendants des orphelins et remettre tous leurs voisins danstodo. (Les voisins d'un orphelin doivent être re-traités car un de leurs voisins a été modifié.)On peut utiliser un parcours en profondeur, et comme nous parcourrons un arbre (
Pred), il ne peut pas y avoir de boucle. Il n'est donc pas nécessaire d'utiliser un tableauVupour ce parcours. (Les tableauxPred,Seenettodocorrespondent aux structures calculées parfind_pathque l'on doit mettre à jour.)void update_Pred(graph* G, size_t Pred[], queue* todo, int Seen[], stack* orphan) { size_t s; while (pop_stack(orphan, &s)) { // on parcourt les voisins de s for (arc* a = G->Adj[s]; a->target != NULL_NODE; a++) { size_t v = a->target; // les voisins à l'extérieur de la forêt Pred sont ignorés car // find_path ne les a pas encore atteints if (Pred[v] == NULL_NODE && !Seen[v]) { continue; } // on déconnecte les fils de s dans Pred, qui deviennent des // orphelins ... // s'il y a une arête (non saturée) de v vers s, le sommet // v doit redevenir actif : find_path va devoir le regarder à // nouveau (on le met dans todo, et il ne doit pas rester // "Vu") ... } // comme le sommet s est déconnecté, la fonction find_path va // devoir le re-traiter remove_from_queue(todo, s); Seen[s] = 0; } }La fonction
remove_from_queueest beaucoup plus lente que les fonctionsenqueueetdequeue. Elle a une complexité en O(n) alors queenqueueetdequeueont une complexité (amortie) en O(1).Pour info, le code supprimé de la fonction
update_Predfait 12 lignes dont 1 ligne vide, 2 lignes réduites à}et 2 lignes de commentaires. -
Déplacez l'initialisation de
PredetSeenfaites dans la fonctionfind_pathdans la fonctionmaxflow. Il ne faut pas réinitialiserPred,Seenettododansfind_pathpour continuer le parcours précédent.Il faut quand même remettre
G->sourcedanstodopour être sûr de commencer le parcours. S'il y est déjà ou qu'il est dansSeen, il sera ignoré. -
Ajouter un appel à
update_predaprès l'appel àaugment_flow.Si j'oublie les commentaires et les messages de log, votre fonction
maxflowdevrait donc ressembler àint maxflow(graph* G, int Seen[]) { stack* orphan = new_stack(); size_t* Pred = malloc(G->nb_nodes * sizeof(size_t)); for (size_t k = 0; k < G->nb_nodes; k++) { Pred[k] = NULL_NODE; } queue* todo = new_queue(); enqueue(todo, G->source); int flow_counter = 0; while (find_path(G, Pred, Seen, todo)) { int flow = find_bottleneck(G, Pred); flow_counter += flow; augment_flow(G, Pred, flow, orphan); update_Pred(G, Pred, todo, Seen, orphan); } free(Pred); free_queue(todo); free_stack(orphan); return flow_counter; } -
Testez la segmentation : vous devriez obtenir les même images que précédemment, mais plus rapidement.
Documentez les gains observés.
Meilleure mise à jour du tableau Pred
On peut conserver certaines parties de l'arbre Pred qui se
retrouvent déconnectées. Si un orphelin s à un voisin
v dans l'arbre Pred t.q. l'arête v ⟶ s
n'est pas saturée, on peut rattacher s à l'arbre. On obtiendrait
par exemple :
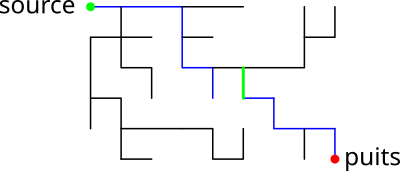
-
Copier votre fichier maxflow-BK0_KURT.c sur maxflow-BK1_KURT.c.
-
Modifiez la chaine
VERSIONen haut du fichier pour préciser que le parcours utilisé est le parcours en largeur basique avec une réutilisation des calculs plus sophistiquée. -
Ajoutez l'optimisation décrite ci dessus dans la fonction
update_Pred. Vous devrez simplement ajouter une boucle avant la gestion d'un orphelinpour tous les voisins v de s si l'arête v ⟶ s n'est pas saturée et si v est rattaché à la source dans l'arbre Pred Pred[s] = v ... ...Bien entendu, il n'est pas nécessaire de continuer à déconnecter le sommet
ssi on a pu le rattacher : il n'est plus orphelin.Pour ceci, vous devrez écrire une fonction auxiliaire qui vérifie si un sommet
vest rattaché à la source. (On ne peut pas simplement vérifier siPred[v] != NULL_NODEcar il pourrait être dans une partie de l'arbre que l'on est en train de déconnecter.) Pour ceci, il suffit de remonter dansPredet de vérifier qu'on tombe surG->sourceavant de tomber surNULL_NODE.Pour info,
-
le corps de ma fonction auxiliaire fait 7 lignes, dont 2 lignes réduites à
}, -
j'ai ajouté 13 lignes dans ma fonction
update_Pred, dont 3 lignes réduites à}.
-
-
Attention, le sommet
G->sinkn'est pas forcément déconnecté de l'arbrePred. Avant de lancer sa boucle principale, la fonctionfind_pathdoit donc vérifier siG->sinkest dans l'arbrePred-
s'il y est,
find_pathpeut directement terminer avec succès ; -
s'il n'y est pas, on fait le parcours normalement.
-
-
Vérifiez que la segmentation fonctionne toujours et documentez les gains de temps observés.
Pour aller plus loin
-
Profilez votre code, et proposez des améliorations possibles.
-
(bonus) Implémentez ces amélioration et documentez les gains observés.
Il n'est pas très difficile, de diviser encore le temps d'exécution par 2 ou 3.

